Mining information using diffusion models

Outline

• Diffusion models
• Overview of distillation techniques
• Diff-mining paper
• Current project/idea

Diffusion models

• A forward process gradually noising an image \(x\): \[ x_t^\epsilon = \sqrt{\alpha_t} x + (1-\sqrt{\alpha_t})\epsilon \]
• A denoiser \(\epsilon_\theta(x_t^\epsilon, t)\)
• Trained by minimizing \[ L_t(x, \epsilon) = ||\epsilon_\theta(x_t^\epsilon, t) - \epsilon||^2 \]
• Optionnally the denoiser \(\epsilon_\theta(x_t^\epsilon, t, c)\) is conditioned on an input \(c\) (e.g. text)

Diffusion models

Diffusion models are generative models that gradually denoise a noisy input

 

Diffusion models: score function

The score of a probability density \(p(x)\) is the derivative of the log-density \(\nabla_x \log p(x)\) (vector field)

Following this vector field is equivalent to sample new examples

Denoising process ~ following the score at different noise levels

 

Main application: text-to-image (memes and jokes)

“A ghibli style photo of the group”

Diffusion models carry out information

“A man”

“A happy man”

“A sad man”

Diffusion models carry out information

“A living room”

“A french living room”

“A japanese living room”

There are many ways to distill or mine this information !

Score distillaton sampling (2D-to-3D)

Score distillation sampling ¹ is a technique for transferring knowledge from a source domain (2D) to a target domain (3D) with

• A trained denoiser on the source domain
• A differentiable representation \(\psi\) on the target domain
• A differentiable function \(x = g(\psi)\) target -> source domain

By “following” the score on the source domain, we can successfully obtain realistic/faithful representation on the target domain

1. Poole et al. DreamFusion: Text-to-3D using 2D Diffusion

Score distillaton sampling (2D-to-3D)

 

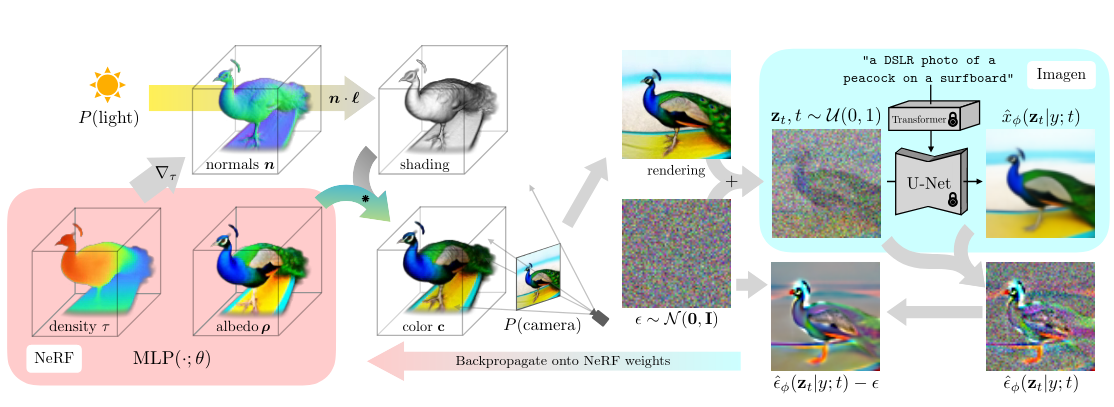
Score distillaton sampling (2D-to-3D)

 

Score distillation (shape matching)

An efficient way to compute matching between shapes is via deep functional maps ¹, that approximates a matching via a functional map matrix C.

Deep functional maps pipeline

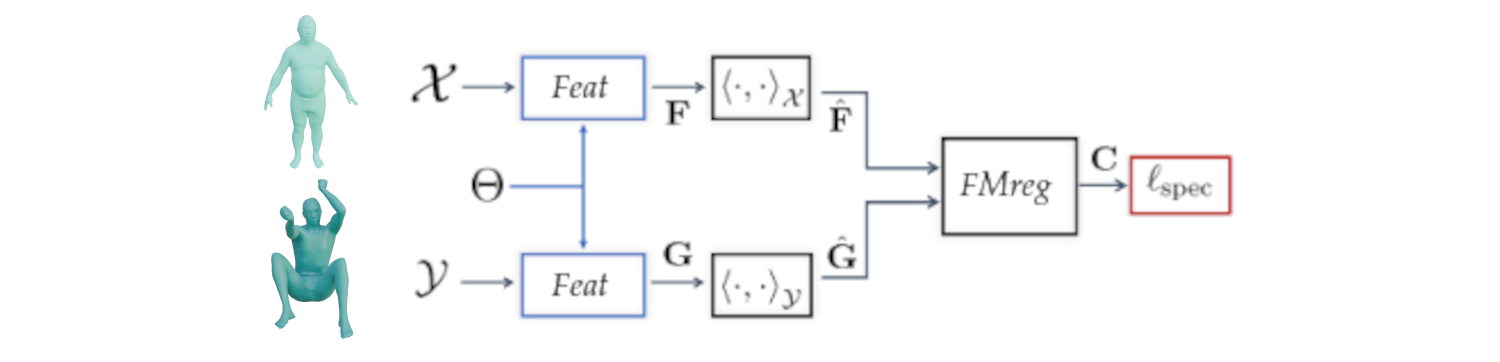
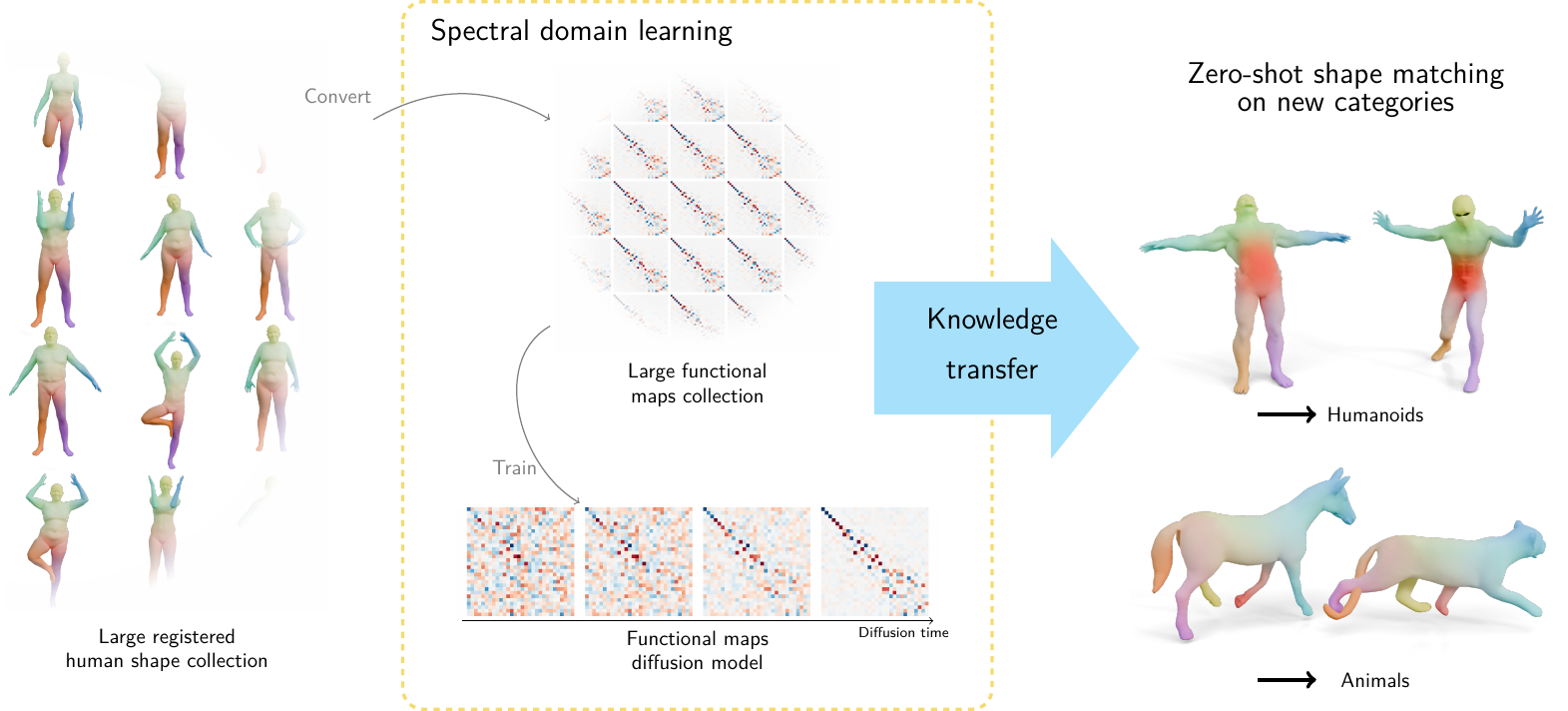
Assuming we have a set of groundtruth functional maps, we can learn a functional maps diffusion model and leverage SDS for zero-shot shape matching!

1. Donati et al. Deep Geometric Functional Maps: Robust Feature Learning for Shape Correspondence

Score distillation (shape matching)

 

Dataset generation/augmentation

DiffusionDB ¹ contains 14 million curated images generated using StableDiffusion

 

1. Wang et al. DiffusionDB: A Large-Scale Prompt Gallery Dataset for Text-to-Image Generative Models

Application : Fine-tuning a Image-to-3D diffusion model

Hi-3DGen ¹ finetunes TRELLIS ², an Image to 3D model, using synthetic detailed Image-3D pairs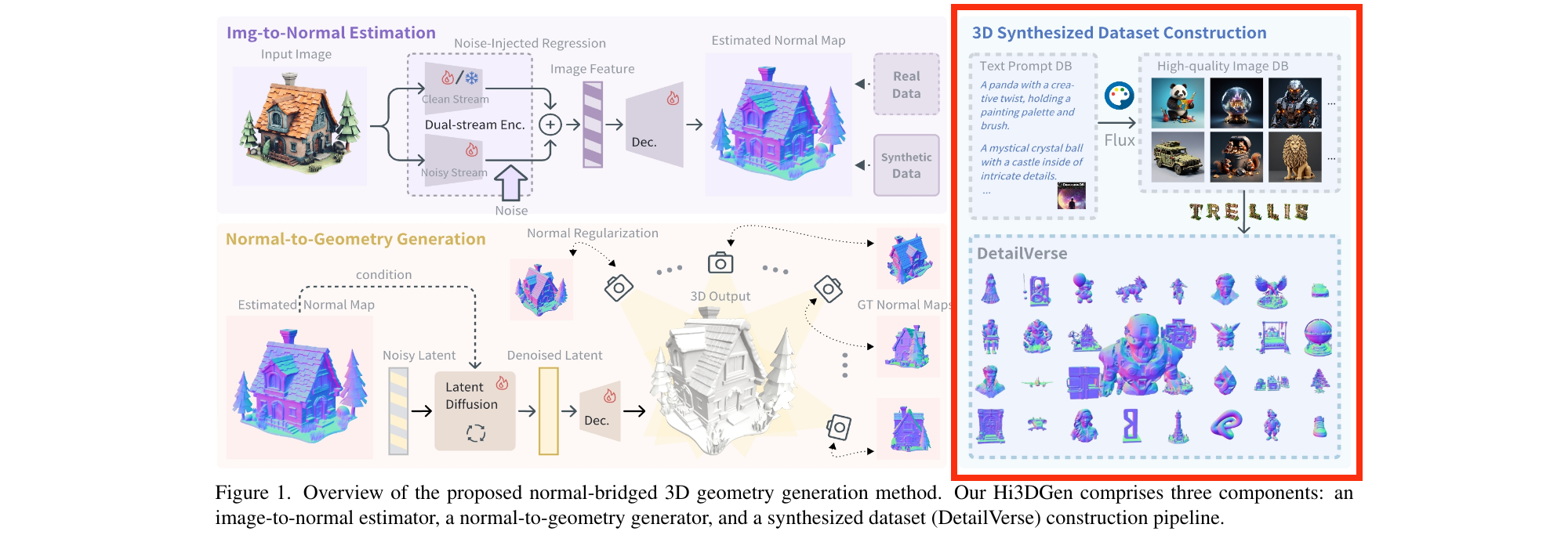

1. Chongjie et al. Hi-3DGen: High-fidelity 3D Geometry Generation from Images via Normal Bridging

2. Xiang et al. Structured 3D Latents for Scalable and Versatile 3D Generation

Application : Fine-tuning a Image-to-3D diffusion model

Hi-3DGen is able to capture finer details from images compared to the initial TRELLIS model

Trellis vs Hi-3DGen

Application: Discovering Human-Object Interaction

CHORUS ¹ learns Human-Object interaction from synthetic images.

 

1. Han et al. CHORUS : Learning Canonicalized 3D Human-Object Spatial Relations from Unbounded Synthesized Images

Image correspondence

Diffusion models implicitly learns correspondences. The features of a trained denoiser can be used for zero-shot image correspondences (no fine-tuning) ¹.

 

1. Luming et al. Emergent Correspondence from Image Diffusion

Diffusion models as data mining tools

Can you guess where the photo comes from?

 

Diffusion models as data mining tools

Answer: USA

 

Mining typical visual elements

Typical visual elements of a location/style/date are:

• discriminative: they distinguish one location from another
• frequent: they appear repeatedly across multiple images of the same location.
• localized (patches)

Diff-mining ¹ proposes a diffusion model based solution.

 

1. Siglidis et al. Diffusion Models as Data Mining Tools

Related work

“What makes Paris look like Paris?” ¹

• Select random patches from Street-View Paris
• Compute features of the patches (HoG)
• Pick k-NN (positive patches) and k negative patches (for each patch) (1)
• Train a classifier from the patches (for each patch)
• Use the learned weights for patch distance and repeat (1)
• Keep the patches with best classifier performance

1. Doersch et al. What makes Paris look like Paris?

Related work

 

Related work : drawbacks

• Needs a different dataset for each location
• Process relatively slow
• Not the best features
• Dataset needs to be curated

 

Diffusion models

• A denoiser \(\epsilon_\theta(x_t^\epsilon, t)\)
• Trained by minimizing \[ L_t(x, \epsilon) = ||\epsilon_\theta(x_t^\epsilon, t) - \epsilon||^2 \]
• Optionnally the denoiser \(\epsilon_\theta(x_t^\epsilon, t, c)\) is conditioned on an input \(c\) (e.g. text)

Diffusion based typicality

“We design our measure of typicality based on the following intuition: a visual element is typical of a conditioning class label (e.g., country name or date) if the diffusion model is better at denoising the input image in the presence of the label than in its absence.”

Typicality is defined as \[ T(x |c) = \mathbb{E}_{\epsilon, t} [L_t(x, \epsilon, \varnothing) - L(x, \epsilon, c)] \]

Typicality

 

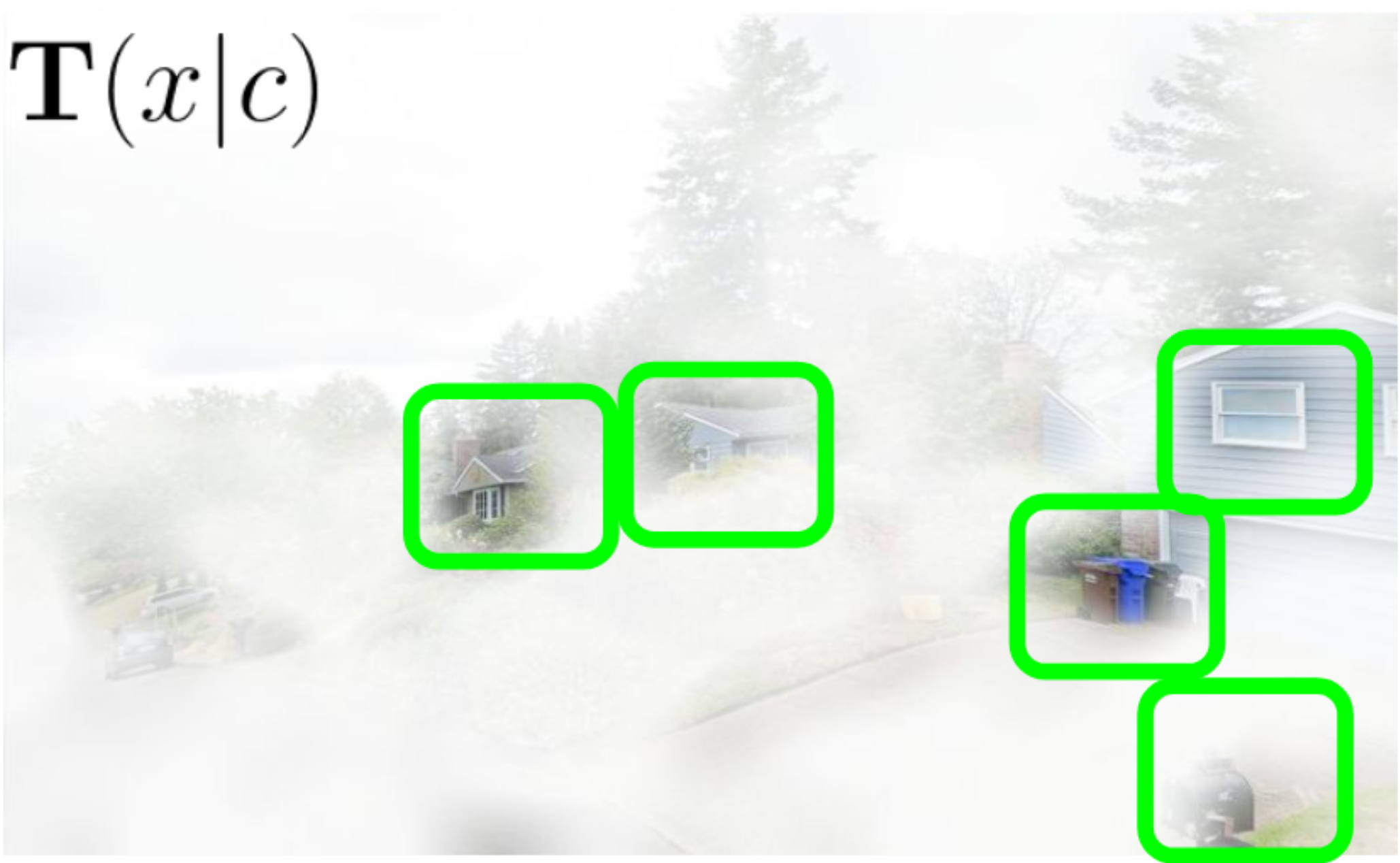
Mining visual elements of a dataset

• Finetuning a diffusion model (Stable Diffusion) on the dataset with class condition (“An image of {label}”)
• Gather most typical images in patches, and keep the 1000 most typical patches in the dataset
• K-Means clustering to obtain 32 patches (using DIFT features)

Results

 

Results

 

Can we lift this idea to 3D?

“Co-Locating Style-Defining Elements on 3D Shapes” ¹

 

1. Hu et al. Co-Locating Style-Defining Elements on 3D Shapes

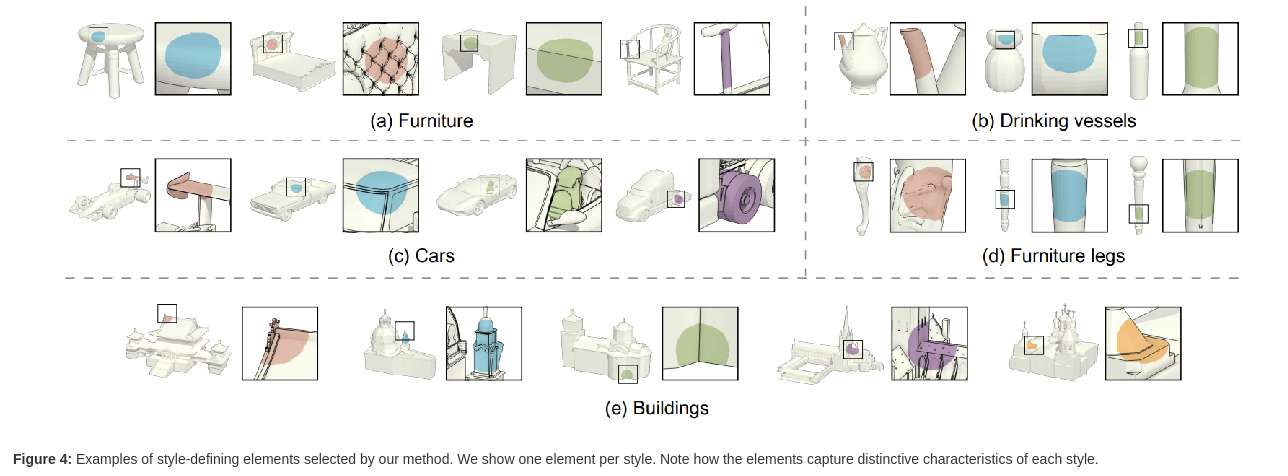
Can we lift this idea to 3D?

Main difficulties/question

• What would be the patch representation?
• Diff-mining is designed for dataset of > 10K images
• No similar dataset for shapes
• Can we generate the dataset ?

Stable diffusion prompt: “A Victorian-era chair crafted from natural wood, featuring carved spindles and a high, elegant back.”