Denoising Diffusion
in the space of functional maps
Objective: Regularization of maps
How can we regularize maps between shapes in a efficient, data-driven way?
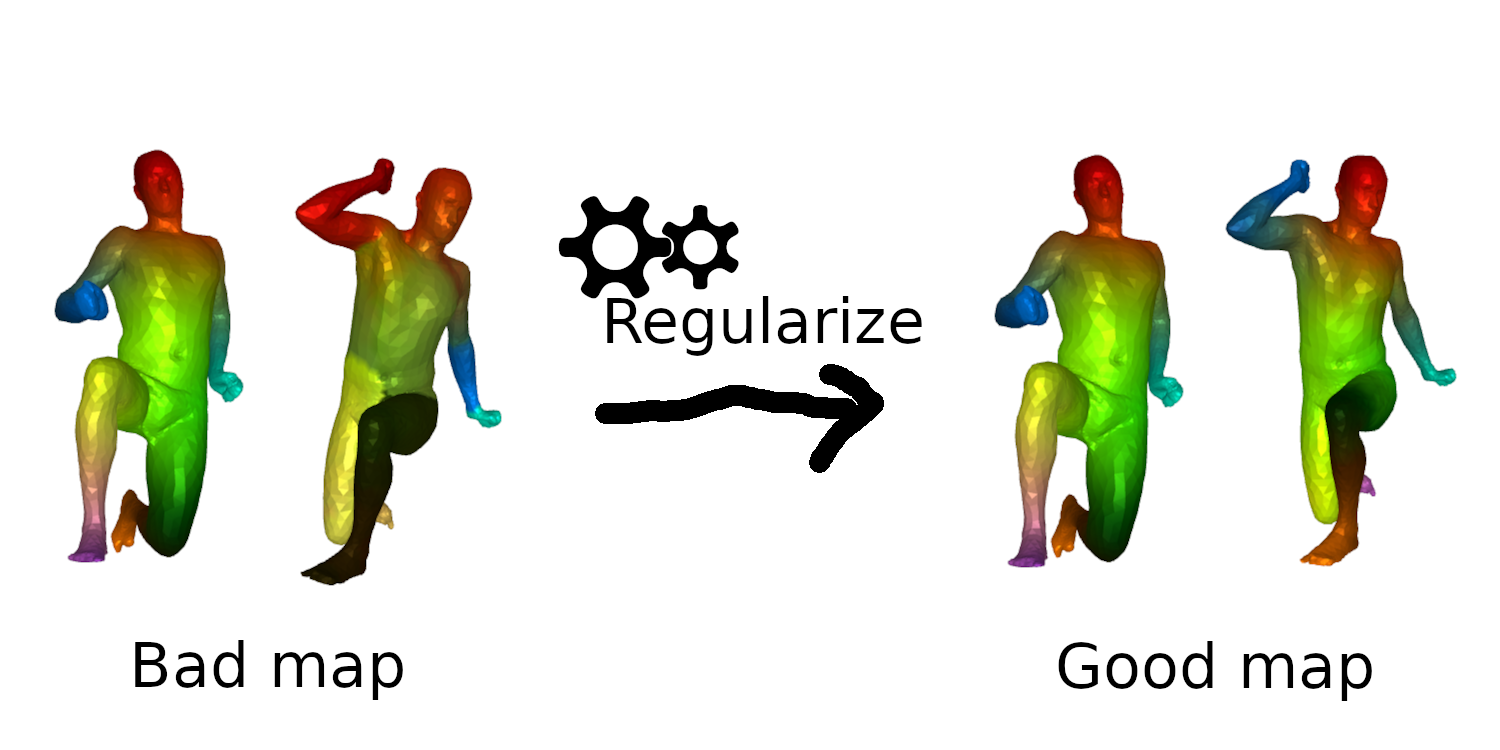 ;
;
Background: Functional maps
Let \(M\), \(N\) two shapes. We aim to find a pointwise map \(T : M \to N\)
The idea is to represent the map as a map \(T_F\) between function spaces \(\mathcal{F}(M, \mathbb{R}) \to \mathcal{F}(N, \mathbb{R})\), such that for \(f: M \to \mathbb{R}\), the corresponding function is \(g = f \circ T^{-1}\).
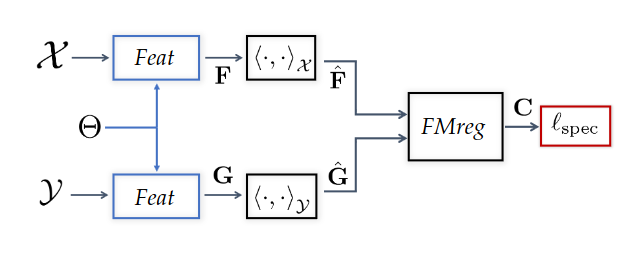
It can be shown that this map is linear. We usually represent it as a mapping matrix C between basis function (Laplace Beltrami eigenfunctions) on M and N (note: a mapping matrix \(C\) does not necessarily correspond to a pointwise map).
The pointwise map is then extracted from the mapping matrix.
Background: Functional maps
Let’s have two shapes that we wan’t to match. The natural basis functions to choose are the Laplace Beltrami Operator (LBO) eigenfunctions. Now, suppose, we know a way to define a set of functions \(f_i\) on \(N\) and \(g_j\) on \(M\) such that \(g(x) \sim f \circ T^{-1} (x)\) (local descriptors which are isometry invariant).
We decompose all \(f_i\) as \(a \in \mathbb{R}^{n \times m}\) and \(g_j\) as \(b \in \mathbb{R}^{n \times m}\). The functional map can be defined as the solution of: \[ C = \underset{C}{\text{argmin}} ||Ca - b||² \]
In practice, we compute the pointwise descriptors using a neural network. Since the output of the previous equation can be obtained in closed form, we optimize the output \(C\) with respect to the ground truth map \(C_{gt}\) or with axiomatic constraints, allowing to learn the descriptors.
New problem
How can we regularize functional maps in a efficient, data-driven way?
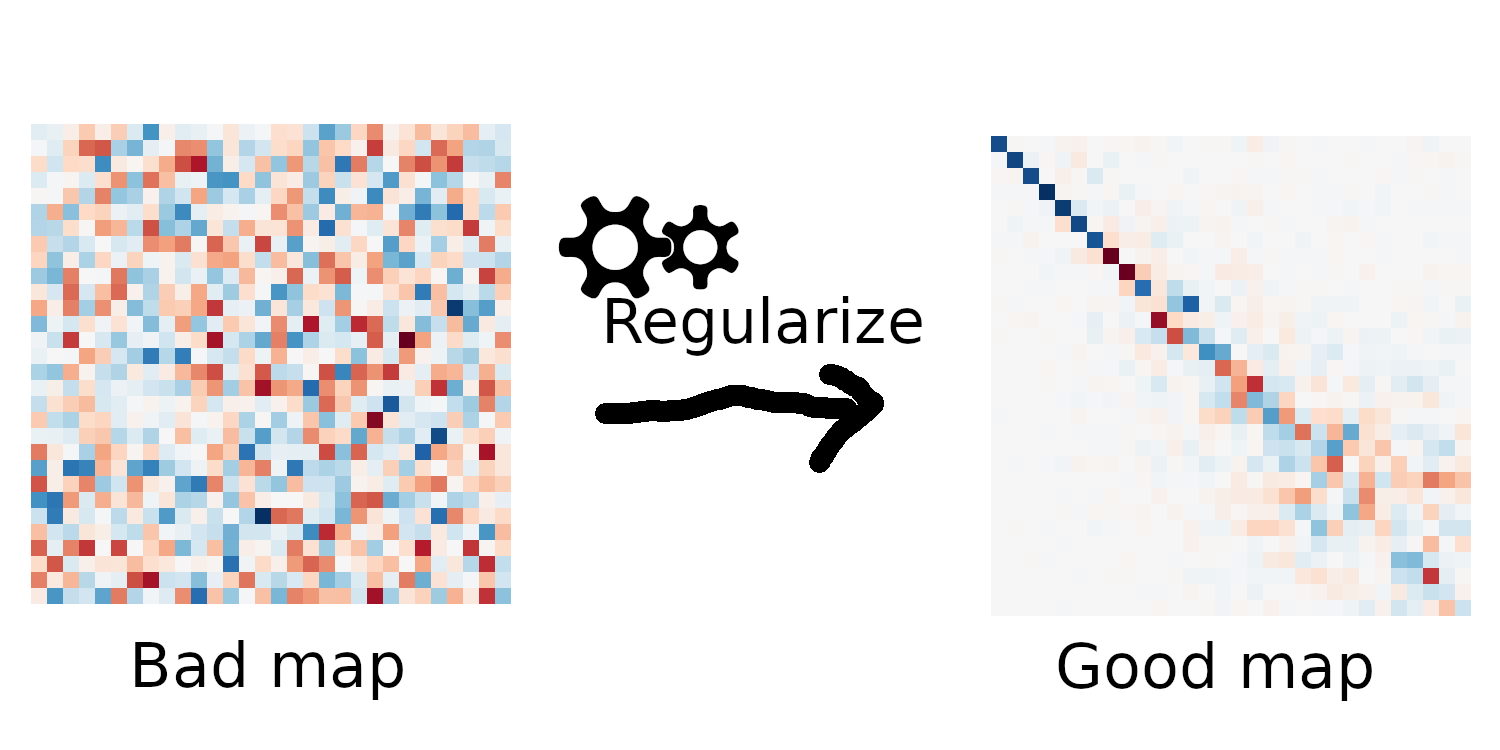 ;
;
Idea: data-driven shape matching
We have access to huge datasets of registered non rigid shapes nowadays.

A few shapes of AMASS. The whole dataset contains around 100 million poses
We can extract the ground truth functional maps to devise a desired structure of maps.
Promising path: denoising diffusion models
Denoising diffusion probabilistic models is currently the “best” way to learn a data distribution (at least on images).

Image diffusion model
Functional map diffusion model
We now train a functional map diffusion model

Functional map diffusion
Some generated maps

Some generated maps
Straightforward approach: Score distillation for functional map regularization.
Quick reminder of the original SDS loss. We have a differentiable way of parameterizing an image \(I\) by some parameters \(\theta\) (NeRF parameters)
The gradient update of the parameters is given by
\[ \nabla \mathcal{L}_{\text{SDS}}(x = g(\theta)) = \mathbb{E}_{t, \epsilon} \left[ \left(\hat{\epsilon}_{\phi}(x_t, t) - \epsilon\right) \frac{dx}{d\theta}\right] \]
Assuming we can define a way of defining the target map \(C\) by some differentiable parameters (FMreg), we can optimize for \(C\) using a fmap diffusion model SDS!
Problem: sign ambiguity

Problem: sign ambiguity

Problem: sign ambiguity

The map on the left is identified as a good map, and changing the sign is too costly!
Simple strategy
We train now a model on “absolute” functional maps \(|C|\), and use the corresponding SDS ((+ some other techniques of distillation)

Absolute functional map
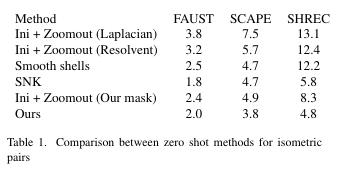
Results
Shape Nonrigid Kinematice (SNK, NIPS 2023) is a state of the art method for zero shot shape matching.
Takeaways
- Yes, diffusion models captures some desired structure of functional maps, and can be used to regularize them
- Sign ambiguity is an important problem to tackle
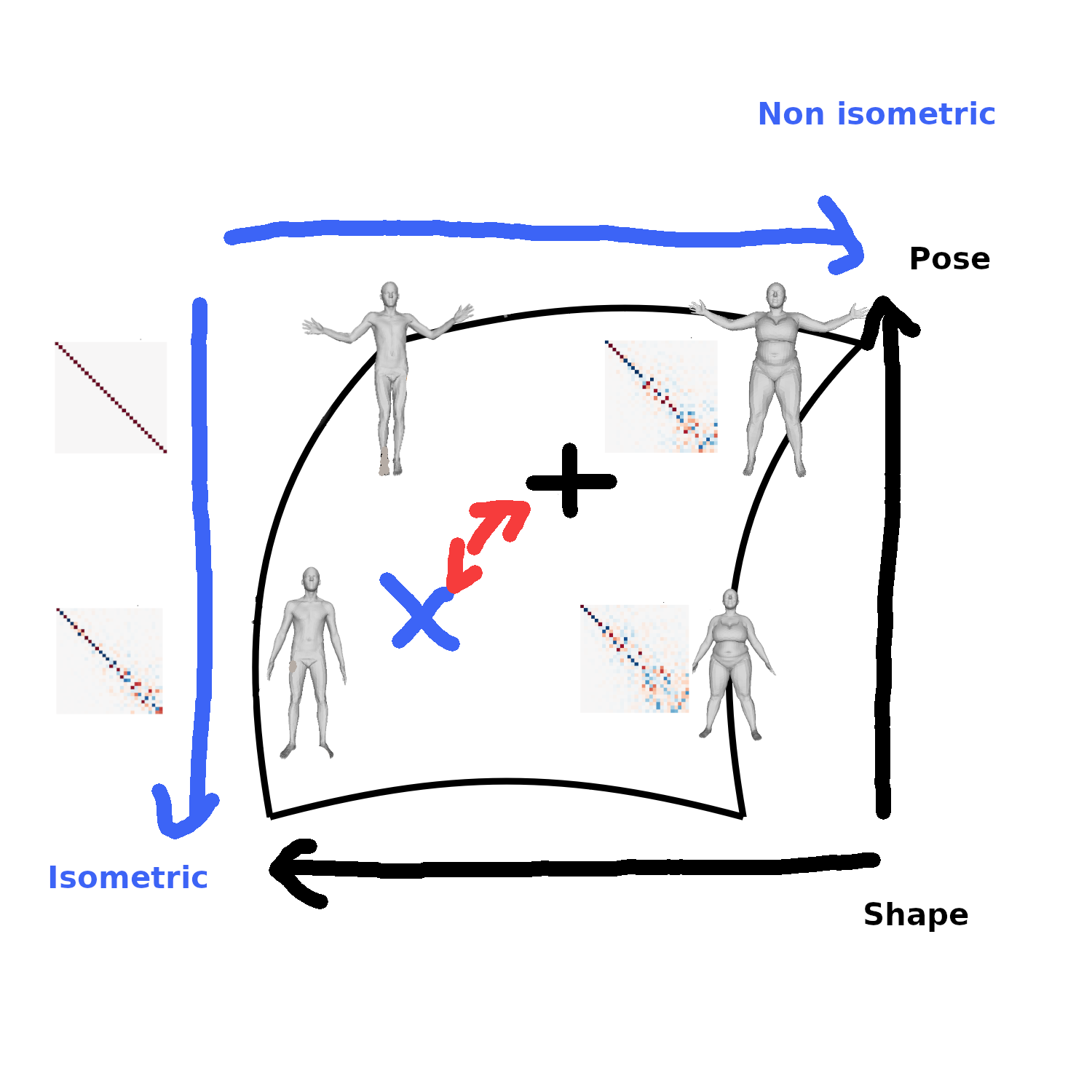
Our project: Compositionality of maps
Discussion/Thoughts
- No work, or little, ha been done on differentiations this way (except in the seminal paper “Shape Differences, 2013”)
- Sign ambiguity will be a problem, but absolute maps have no compositionality
- The adjoint operator \(C C^T\), does not have sign ambiguity, and has been studied in “Shape Differences, 2013”
More Discussion
A potential easy application is motion registration:
