## {.smaller} ### Last suggestions Instead of working by optimizing SDS Loss directly, the experiment consists of searching whereas we can use the transferred vertices to recover the ground truth functional map. Let $\mathcal{S}$ the input shapes, $\mathcal{T} the template shape, $C$ the functional map matrix. We suppose we are given a way to transfer the coordinates of $S$, $X_\mathcal{S}$, to $X_{S \to T}$ using $C$. The transfer function is denoted $F(X_S, C)$. We suppose we know $X_{S \to T}^{\text{gt}} = F(X_S, C_{\text{gt}})$. Starting from a noisy $C$, can we recover $C_{\text{gt}}$ from $X_{S \to T}^{\text{gt}}$, by minimizing the loss below ? $$ || F(X_S, C) - X_{S \to T}^{\text{gt}} || ² $$ ## ### Experiments Now, there a 3 different ways of transferring the data: - "Matrix transfer": $F(X_S, C) = \phi_T C \phi_S^T X_S$ (transferring in Laplacian basis directly) - "Distance transfer": $F(X_S, C) = \Pi_{S \to T}^C X_S$, where $\Pi_{S \to T}^C (p, q) = Softmax(\delta_{pq})$, where $\delta_{pq} = ||\Phi_T(q) - C\Phi_S(p)||²$ - "Product transfer" $F(X_S, C) = \Pi_{S \to T}^C X_S$ where now $\delta_{pq} = \frac{\langle \Phi_T(q), C\Phi_S(p) \rangle}{|| \Phi_T(q)|| || C\Phi_S(p)||}$ ## Input shape The results are shown for the following input shape, but behavior is the same with other examples 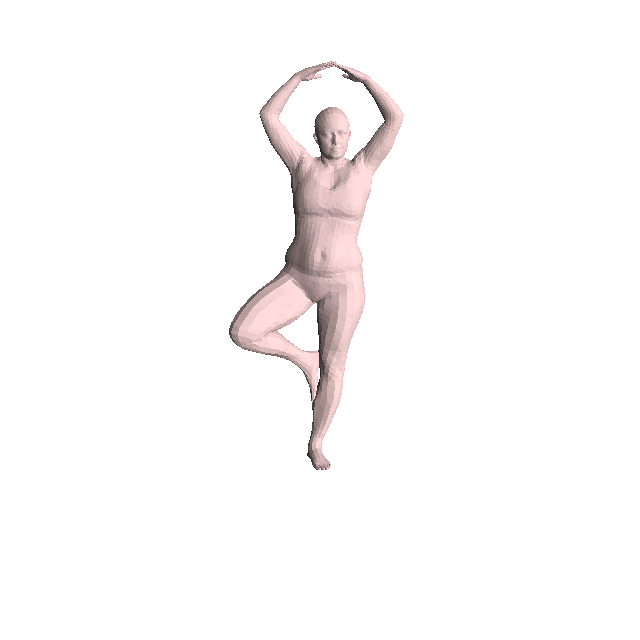 ## Matrix transfer From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map.  ## Distance transfer From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map.  ## Product transfer From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map.  ## Adding a new term We now add a new term to the loss we want to minimize. Given the transferred vertices $X_{\mathcal{S} \to \mathcal{T}}$, we compute the point correspondance in the spatial coordinates (based on distances, which makes more sense). We then extract a functional map based on this correspondance, $C_{\text{spatial}}$, and minimize: $$ || C - C_{\text{spatial}}||^2 $$ ## Matrix transfer From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map.  ## Distance transfer From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map.  ## Product transfer From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map. 