Non rigid diffusion:
Application to shape matching
### Objective: data-driven shape matching {.smaller} ::: columns ::: {.column width="50%" .r-fit-text} Final objective: shape matching 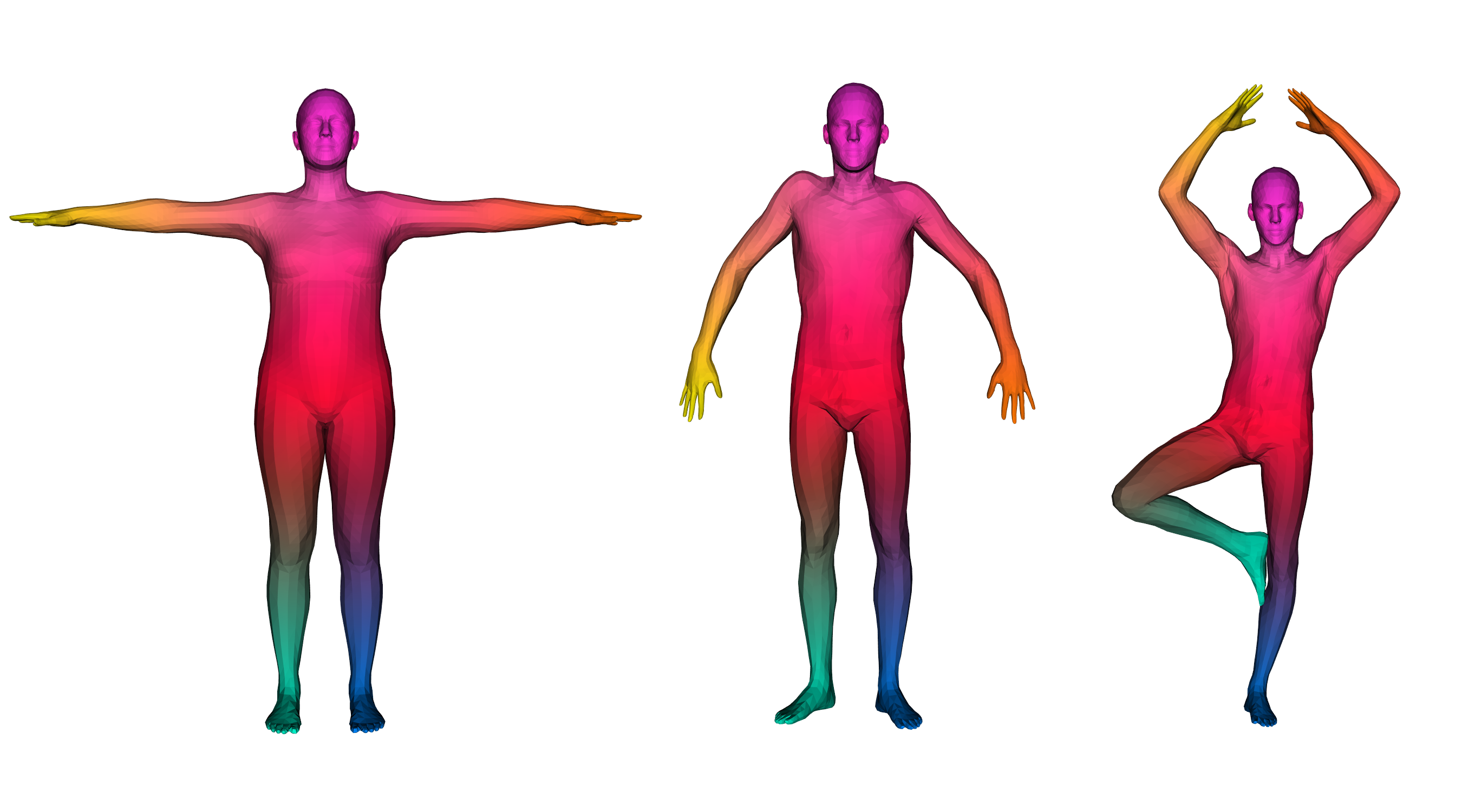 ::: ::: {.column width="50%" .r-fit-text} We have access to huge datasets of non rigid shapes nowadays.  ::: ::: The objective is to take profit of some huge databases of non rigid shapes to improve shape matching algorithms. ## {.smaller} ### Shape matching algorithms are not perfect {.smaller} A general problem in non rigid shape matching is dealing with symmetries. Regularizing algorithms with axiomatic constraints are not sufficient to get rid of this problem. ![Example of a map where some parts of the arms are switched because of the natural symmetry of the human body. In gray, the template shape, in pink the target shape and in blue the target shape with connectivity transferred from the template shape via functional maps extracted using [@li2022learning]](images/symmetries.png){.nostretch fig-align="center" width="600"} Is there a data-driven way to regularize the functional map and solve this problem ? ## Background: Functional maps {.smaller} Let $M$, $N$ two shapes. We aim to find a pointwise map $T : M \to N$ The idea is to represent the map as a map $T_F$ between function spaces $\mathcal{F}(M, \mathbb{R}) \to \mathcal{F}(N, \mathbb{R})$, such that for $f: M \to \mathbb{R}$, the corresponding function is $g = f \circ T^{-1}$. It can be shown that this map is linear. We usually represent it as a mapping matrix C between basis function (Laplace Beltrami eigenfunctions) on M and N (note: a mapping matrix $C$ does not necessarily correspond to a pointwise map). The pointwise map is then extracted from the mapping matrix. ## Background: Functional maps {.smaller .scrollable .nostretch} Let's have two shapes that we wan't to match. The natural basis functions to choose are the Laplace Beltrami Operator (LBO) eigenfunctions. Now, suppose, we know a way to define a set of functions $f_i$ on $N$ and $g_j$ on $M$ such that $g(x) \sim f \circ T^{-1} (x)$ (local descriptors which are isometry invariant). We decompose all $f_i$ as $a \in \mathbb{R}^{n \times m}$ and $g_j$ as $b \in \mathbb{R}^{n \times m}$. The functional map can be defined as the solution of: $$ C = \underset{C}{\text{argmin}} ||Ca - b||² $$ In practice, we compute the pointwise descriptors using a neural network. Since the output of the previous equation can be obtained in closed form, we optimize the output $C$ with respect to the ground truth map $C_{gt}$ or with axiomatic constraints, allowing to learn the descriptors 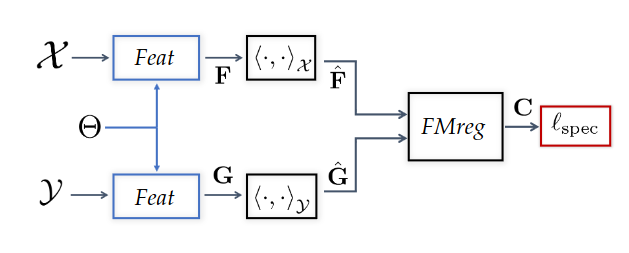{width=600} ## ### Promising path: denoising diffusion models Denoising diffusion probabilistic models is currently the best way to learn a data distribution. Starting point: learn a diffusion model on a set of already aligned non rigid shapes 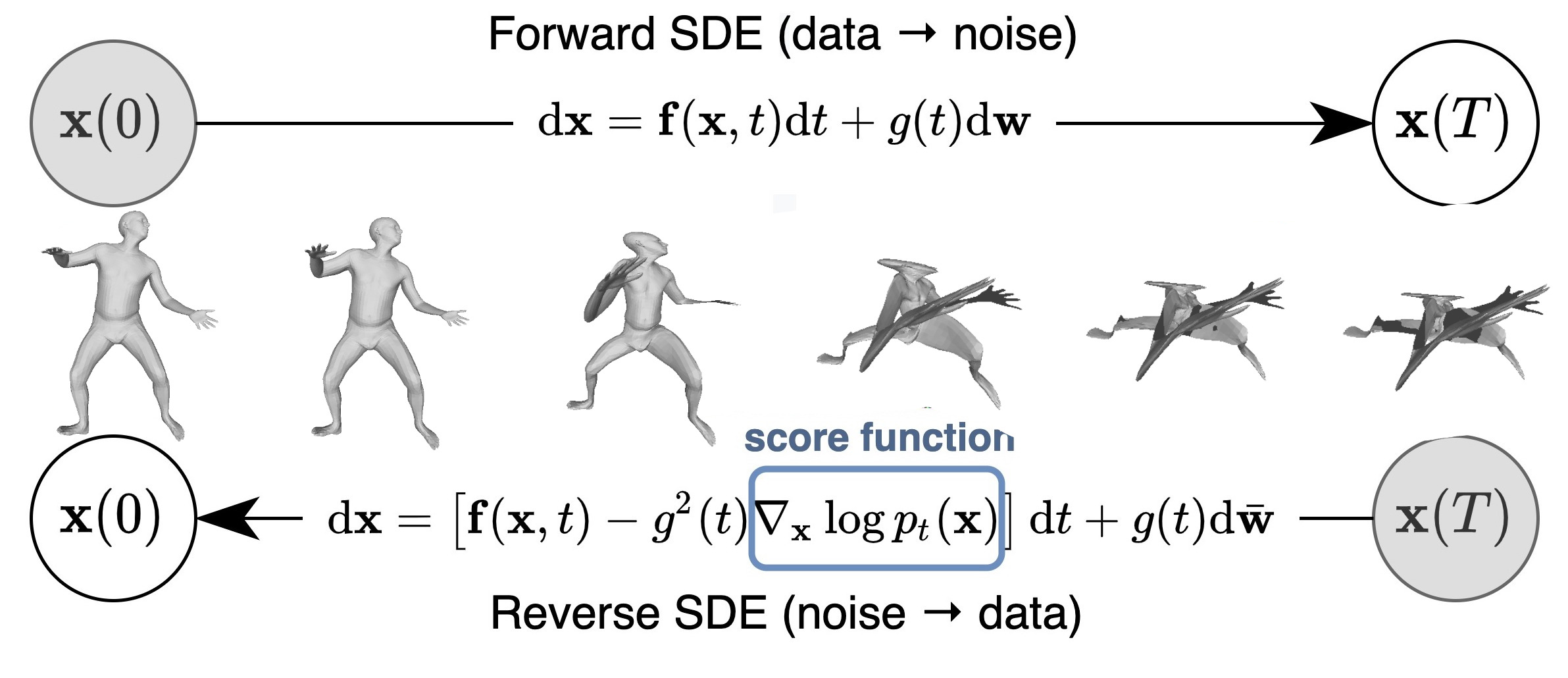 ## {.smaller} ### Shape representation as PCA coefficients Advantages: - low dimensional ($\sim 100$ coefficients vs. $>15000$ points on human shapes) - fast and "exact" recovery of PCA coefficients from shape/shape from PCA coefficients - Recovery from Laplacian basis projection 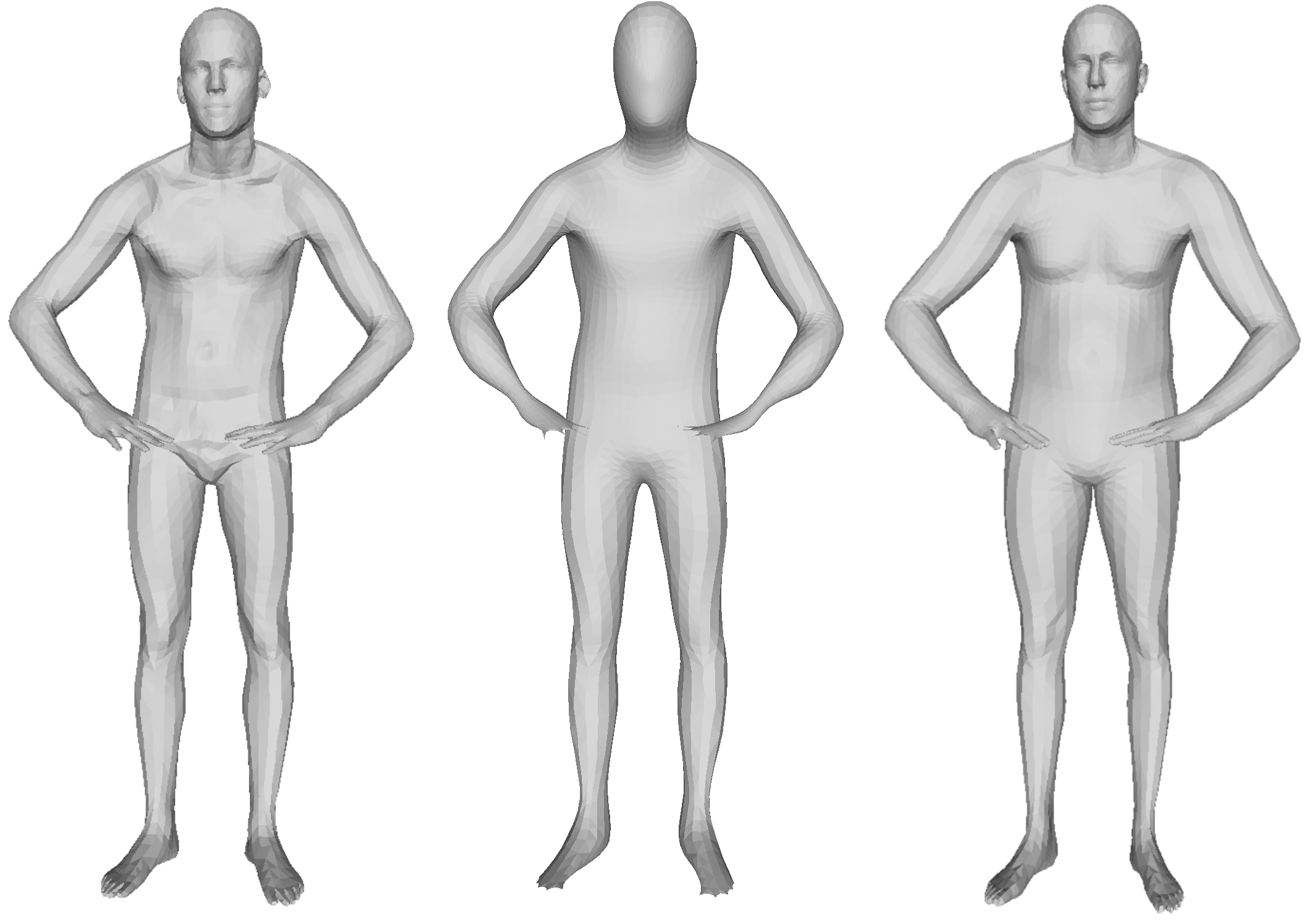{.nostretch fig-align="center" width="400"} We learn a diffusion model on the set of PCA coefficients ## Generative model results {.smaller} Some generated shapes and their nearest neighbor in the training dataset {width=300} The data distribution seems to be approximated well with this approach ## {.smaller} ### Proposed approach: Score distillation for functional map regularization. Quick reminder of the original SDS loss. We have a differentiable way of parameterizing an image $I$ by some parameters $\theta$ (NeRF parameters) The gradient update of the parameters is given by $$ \nabla \mathcal{L}_{\text{SDS}}(x = g(\theta)) = \mathbb{E}_{t, \epsilon} \left[ \left(\hat{\epsilon}_{\phi}(x_t, t) - \epsilon\right) \frac{dx}{d\theta}\right] $$ Assuming we can define a way of transferring the target shape coordinates to the PCA coefficients space using the mapping matrix $C$, such that it is differentiable with respect to $C$, we can optimize for $C$ using the SDS loss (we replace $\theta$ by $C$)! For the moment, we suppose we are given a good initial map $C$. ## Results with naïve approach We transfer the coordinates by seeing them as functions over the shapes, using the mapping matrix.  The SDS loss points towards the mean shape of the dataset, and the approach generates bad deformations. However, the pointwise map remain (almost) unchanged. ## Last results We transfer the coordinates using an extracted pointwise map from the mapping matrix instead of using the matrix directly  It corrects the symmetry, but affects the pointwise map ## Discussion - Can we avoid being pulled too much to the mean shape of the dataset (oversmoothing effect) ? - What if we train a conditioned (with PointNet based autoencoder) diffusion model? - We could also directly train a functional map diffusion model ## The end