Non rigid diffusion, last experiments
Small recap
Let an input shape \(\mathcal{S}\), we wish to find the correspondance between this shape and a template shape \(\mathcal{T}\).
We do it using functional map. A functional map is a linear map between the function space \(\mathcal{S} \to \mathbb{R}\) and \(\mathcal{T} \to \mathbb{R}\).
Let \(\Phi_\mathcal{S} \in \mathbb{R}^{n \times n_S}\), \(\Phi_\mathcal{T} \in \mathbb{R}^{n \times n_T}\), the Laplace eigenvectors of both shapes. The functional map can be represented as a matrix \(C\) taking coefficient in \(S\) basis to the ones in \(T\) basis.
Functional map work by matching features in the eigenbasis, but often fails because of underlying symmetry
Suppose now we have a shape diffusion model (here it is in PCA coefficient space). Can we regularize those results with diffusion models?
Proposed approach
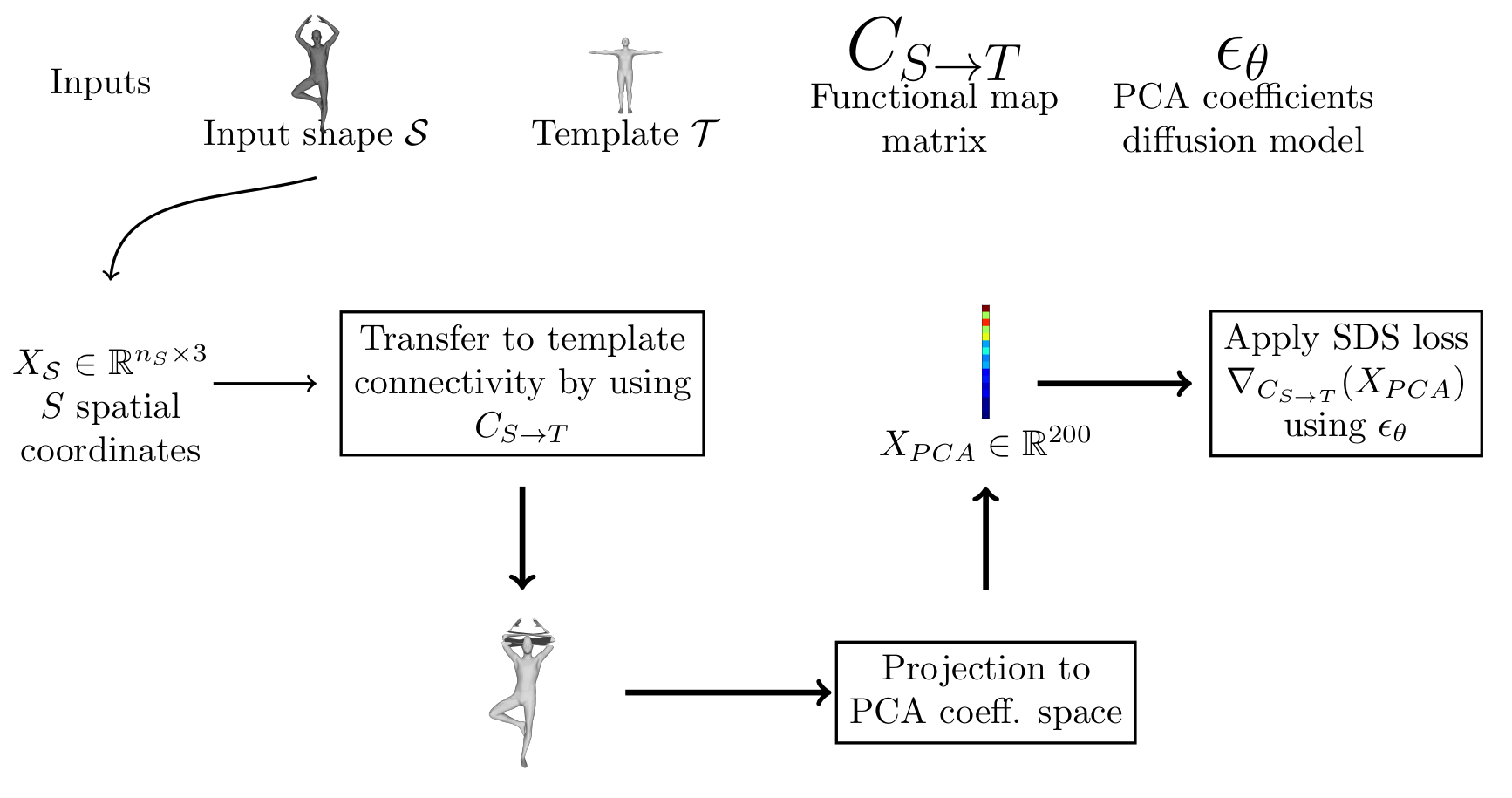 ;
;
Transfer to template connectivity
We transfer the coordinates by convert the matrix \(C_{S \to T}\) to a point to point map \(\Pi_{S \to T}\).
\[ F(X_S, C) = \Pi_{S \to T}^C X_S, \] where \[ \Pi_{S \to T}^C (p, q) = \frac{\exp(-\delta_{pq}*\alpha)}{\sum_q {\exp(-\delta_{pq}*\alpha)}}, \]
with \(\delta_{pq} = ||\Phi_T(q) - C\Phi_S(p)||²\)
Last week results
Remarks of last week
Train a pose + shape model -> changed
What happens with a ground-truth fmap?
Other experiments with ground-truth
Add some usual functional maps loss (orthogonality/others)
First experiment: replace SDS with ground-truth
Given our transfer function \(F(X_S, C)\) we suppose we know \(X_{S \to T}^{\text{gt}} = F(X_S, C_{\text{gt}})\). Starting from a noisy \(C\), can we recover \(C_{\text{gt}}\) from \(X_{S \to T}^{\text{gt}}\), by minimizing the loss below ?
\[ || F(X_S, C) - X_{S \to T}^{\text{gt}} || ² \]
No. But if we add a new term to the loss we want to minimize. Given the transferred vertices \(X_{\mathcal{S} \to \mathcal{T}}\), we compute the point correspondance in the spatial coordinates (+normals, to avoid erros when parts are gluing to each other). We then extract a functional map based on this correspondance, \(C_{\text{spatial}}\), and minimize:
\[ \mathcal{L}_{proper} = || C - C_{\text{spatial}}||^2 \]
With this supplementary loss, the functional map converges.
Example
From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map.
No additional loss:
Additional loss \(\mathcal{L}_{proper}\):
Full losses
We also force the PCA reconstruction to be close to the converted vertices.
\[ \mathcal{L}_{res} = ||\text{Rec}(X_{PCA}) - X_{S \to T} ||² \]
Finally, we encourage the matrix to be orthogonal (~ area preserving map) via
\[ \mathcal{L}_{ortho}= || CC^T - I||^2 \]
The full loss optimized is:
\[ \mathcal{L}_{SDS} + \mathcal{L}_{proper} + \mathcal{L}_{res} + 0.1 * \mathcal{L}_{ortho} \]
Algorithm
 ;
;
Results : starting from ground truth

From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map
Results: starting from output of fmap algorithm
From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map
Results: different identity, easy pose
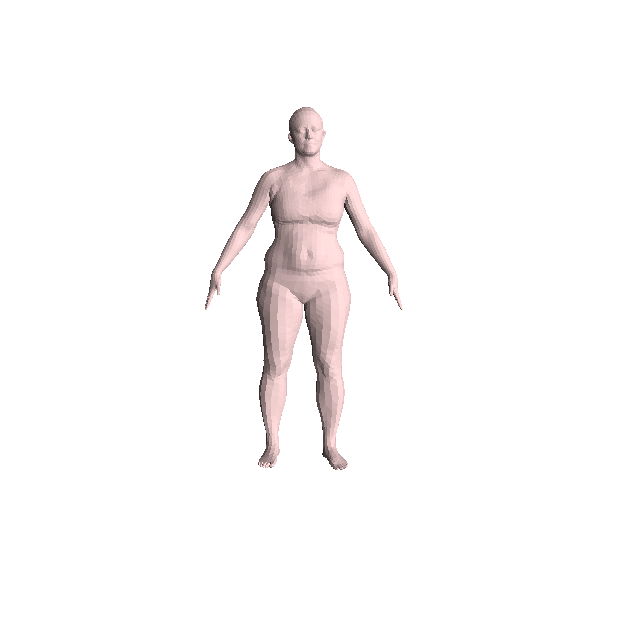
From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map
Results: different identity, hard pose

From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map
Next steps
Theoretical investigations
Quantitative evaluation?
Different application?
Different dataset?