Non rigid diffusion, last experiments
## {.smaller} ### Small recap Let an input shape $\mathcal{S}$, we wish to find the correspondance between this shape and a template shape $\mathcal{T}$. We do it using functional map. A functional map is a linear map between the function space $\mathcal{S} \to \mathbb{R}$ and $\mathcal{T} \to \mathbb{R}$. Let $\Phi_\mathcal{S} \in \mathbb{R}^{n \times n_S}$, $\Phi_\mathcal{T} \in \mathbb{R}^{n \times n_T}$, the Laplace eigenvectors of both shapes. The functional map can be represented as a matrix $C$ taking coefficient in $S$ basis to the ones in $T$ basis. Functional map work by matching features in the eigenbasis, but often fails because of underlying symmetry Suppose now we have a shape diffusion model (here it is in PCA coefficient space). Can we regularize those results with diffusion models? ## Proposed approach 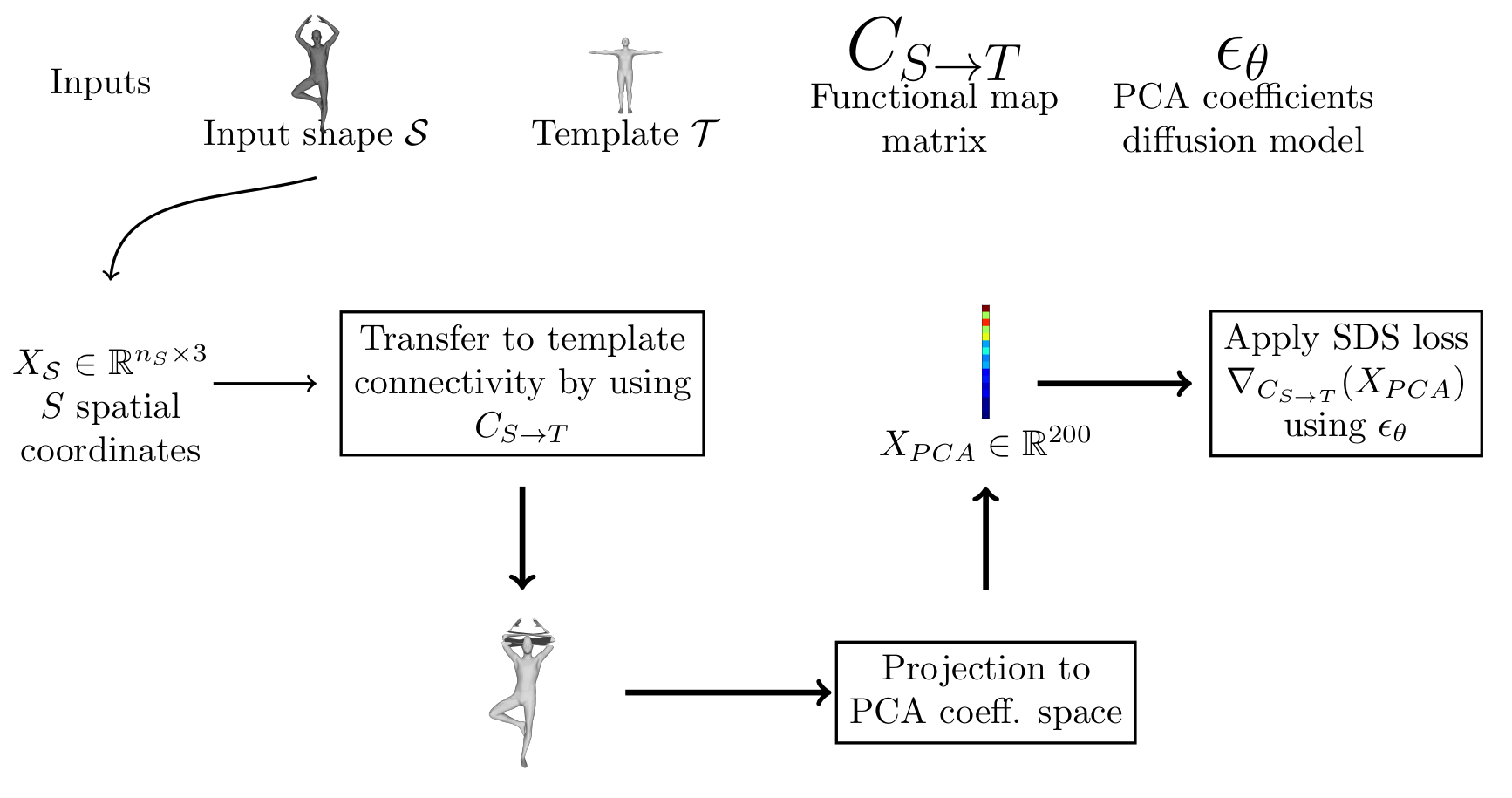; ## Transfer to template connectivity We transfer the coordinates by convert the matrix $C_{S \to T}$ to a point to point map $\Pi_{S \to T}$. $$ F(X_S, C) = \Pi_{S \to T}^C X_S, $$ where $$ \Pi_{S \to T}^C (p, q) = \frac{\exp(-\delta_{pq}*\alpha)}{\sum_q {\exp(-\delta_{pq}*\alpha)}}, $$ with $\delta_{pq} = ||\Phi_T(q) - C\Phi_S(p)||²$ ## Last week results  ## Remarks of last week Train a pose + shape model -> changed What happens with a ground-truth fmap? Other experiments with ground-truth Add some usual functional maps loss (orthogonality/others) ## {.smaller} ### First experiment: replace SDS with ground-truth Given our transfer function $F(X_S, C)$ we suppose we know $X_{S \to T}^{\text{gt}} = F(X_S, C_{\text{gt}})$. Starting from a noisy $C$, can we recover $C_{\text{gt}}$ from $X_{S \to T}^{\text{gt}}$, by minimizing the loss below ? $$ || F(X_S, C) - X_{S \to T}^{\text{gt}} || ² $$ No. But if we add a new term to the loss we want to minimize. Given the transferred vertices $X_{\mathcal{S} \to \mathcal{T}}$, we compute the point correspondance in the spatial coordinates (+normals, to avoid erros when parts are gluing to each other). We then extract a functional map based on this correspondance, $C_{\text{spatial}}$, and minimize: $$ \mathcal{L}_{proper} = || C - C_{\text{spatial}}||^2 $$ With this supplementary loss, the functional map converges. ## Example {.scrollable} From left to right: transferred vertices, texture map, map matrix (first 40 coordinates), distance to ground truth functional map. No additional loss:  Additional loss $\mathcal{L}_{proper}$:  ## Full losses {.smaller} We also force the PCA reconstruction to be close to the converted vertices. $$ \mathcal{L}_{res} = ||\text{Rec}(X_{PCA}) - X_{S \to T} ||² $$ Finally, we encourage the matrix to be orthogonal (~ area preserving map) via $$ \mathcal{L}_{ortho}= || CC^T - I||^2 $$ The full loss optimized is: $$ \mathcal{L}_{SDS} + \mathcal{L}_{proper} + \mathcal{L}_{res} + 0.1 * \mathcal{L}_{ortho} $$ ## Algorithm ; ## {.scrollable .nostretch} ### Results : starting from ground truth {width=600} From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map  ## ### Results: starting from output of fmap algorithm From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map  ## {.scrollable .nostretch} ### Results: different identity, easy pose  From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map  ## {.scrollable .nostretch} ### Results: different identity, hard pose {.scrollable}  From left to right: Reconstruction from PCA coefficients, Transferred vertices, texture map  ## Next steps - Theoretical investigations - Quantitative evaluation? - Different application? - Different dataset? ## Notes for next steps