Denoising diffusion using Stochastic Differential Equations

LIX Seminar

Reminders: score modeling

The score function of a probability distribution with density \(p(x)\) is the gradient of the log-density: \[ \nabla_x \log p(x) \]

Working with this quantity has several advantages:

• Bypasses the normalizing constant problem
• Allows for sampling using Langevin algorithm
• It is possible to learn \(s_\theta(x) \sim \nabla_x \log p(x)\)

Evolution of the score modeling approach

Initial proposal: score matching(Hyvärinen and Dayan 2005)

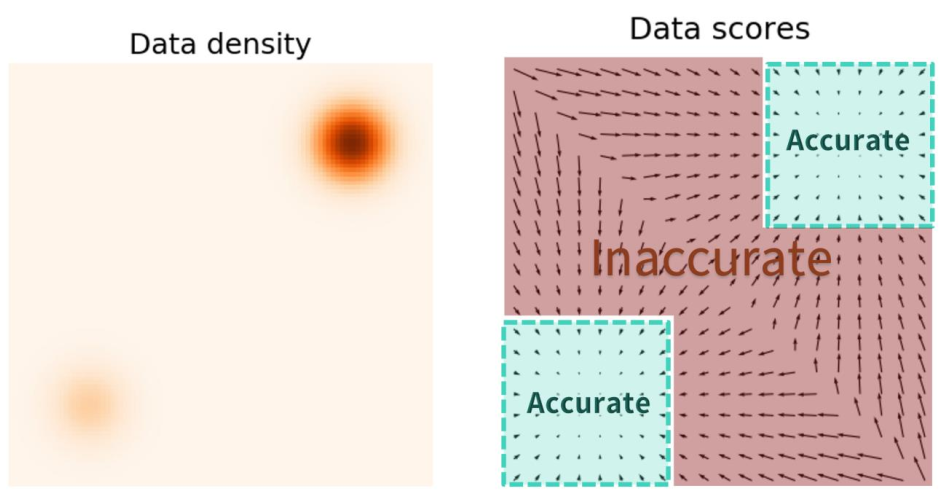
The quantity \(Trace\left(\nabla_x^2 \log p_\theta(x)\right)\) is difficult to compute

The score is untractable in low density areas

Given \(\{x_1, x_2, ..., x_T\} \sim p_\text{data}(x)\) Objective: Minimize the quantity \[ E_{p(x)}\left[\frac{1}{2}|| \log p_{\theta}(x)||² + Trace\left(\nabla_x^2 \log p_\theta(x)\right)\right]\]

 

Evolution of the score modeling approach

Initial proposal: score matching(Hyvärinen and Dayan 2005)

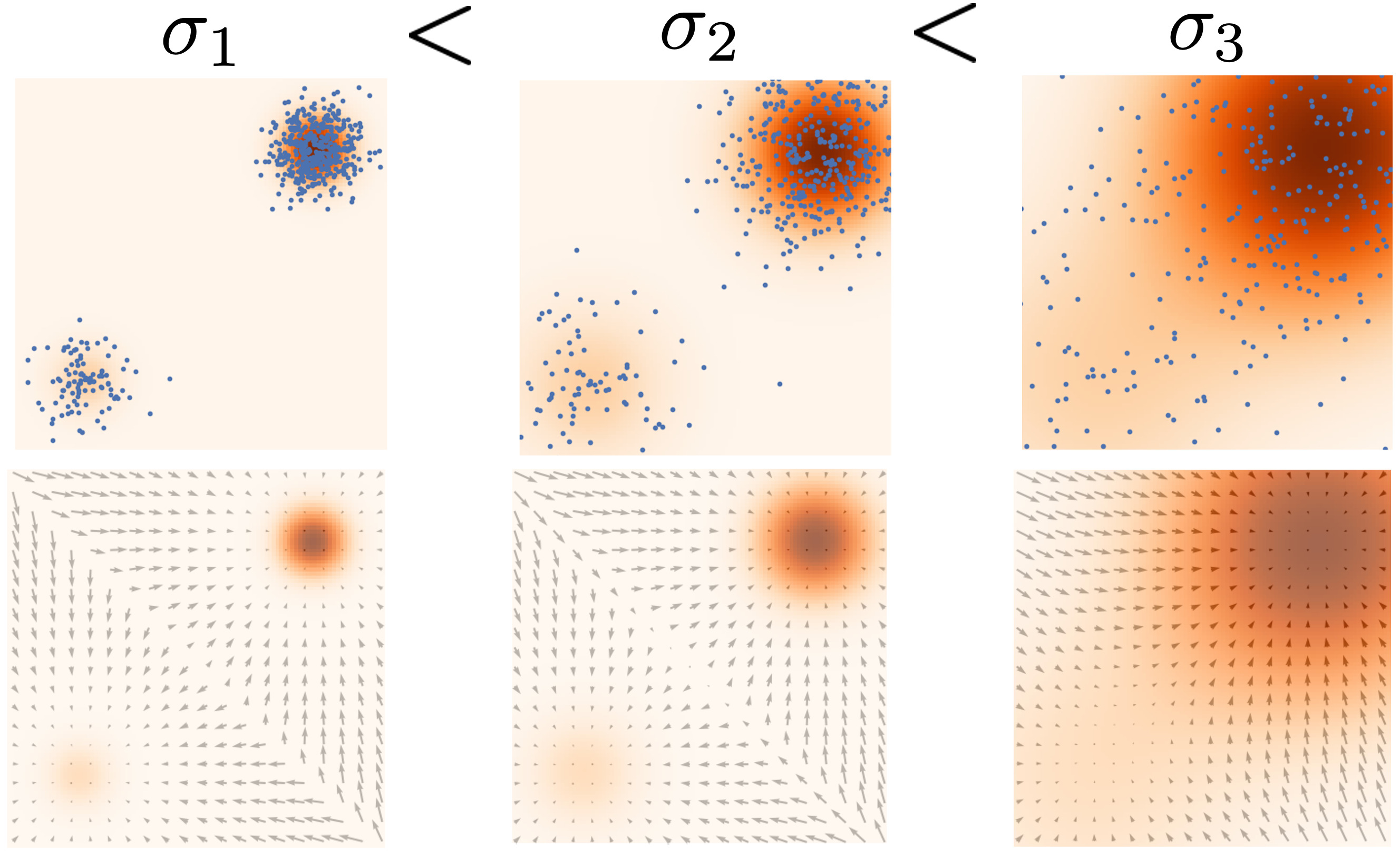
Learning the score of a noisy distribution(Vincent 2011)

No score of noise-free distribution

Noisy distribution

Loss: \(\mathbb{E}\left[\frac{1}{2}\left|\left| s_\theta(\tilde{x})- \frac{\tilde{x}-x}{\sigma²}\right|\right|²\right]\)

Evolution of the score modeling approach

Initial proposal: score matching(Hyvärinen and Dayan 2005)

Learning the score of a noisy distribution(Vincent 2011)

Denoising diffusion models(Sohl-Dickstein et al. 2015), annealed Langevin dynamics(Y. Song and Ermon 2019)

• Gradually decrease noise in the distribution
• Can obtain non noisy samples

Annealed Langevin sampling

Noise conditional score model, with objective : \[ \frac{1}{L} \sum_{i=1}^L \lambda(\sigma_i) \mathbb{E}\left[\left\lvert\left\lvert s_\theta(x_i, \sigma_i) - \frac{(\tilde{x}_i - x_i)}{\sigma_i²}\right\rvert\right\rvert ² \right] \]

Evolution of the score modeling approach

Initial proposal: score matching(Hyvärinen and Dayan 2005)

Learning the score of a noisy distribution(Vincent 2011)

Denoising diffusion models(Sohl-Dickstein et al. 2015), annealed Langevin dynamics(Y. Song and Ermon 2019)

DDPM beats GAN(Ho, Jain, and Abbeel 2020)!

 

What is DDPM?

• Forward process \(x_t = \sqrt{1-\beta_t} x_{t-1} + \sqrt{\beta_t} z_t\)
• A denoiser \(\epsilon_\theta(., t)\), parameterizing the score function
• Backward process \(x_{t-1} = \frac{1}{\sqrt{1-\beta_t}} \left(x_t - \frac{\beta_t}{\sqrt{1-\alpha_t\alpha_{t-1}}}\epsilon_\theta(x_t, t)\right) + \sigma_t z_t\)
• A simple training objective \(L_\text{simple}=\left|\left|\epsilon-\epsilon_\theta\left(\underbrace{\sqrt{\bar{\alpha_t}}x_0+\sqrt{1-\bar{\alpha_t}}\epsilon}_{\text{Forward estimate of } x_t \text{ given } x_0},t\right)\right|\right|^2\)
• This objective is equivalent to the denoising score matching objective

Algorithm

 

Questions/Problems

• Can we unify DDPM and other approaches in a common framework?
• Number of timesteps \(T\) needs to be fixed before training
• Can we fasten the sampling, ideally without needed re-training?
• Can we model the data in a deterministic way using score modeling?

Proposed solution: Score modeling using Stochastic Differential Equations(Y. Song et al. 2021)!

Ordinary Differential Equations (ODE)

Equations of functions, of the form \(\frac{dx}{dt} = f(x, t)\) (order 1).

• Unique solution for any initial condition \(x(t_0)\)
• Geometric interpretation using vector fields

Stochastic diffential equations (SDE)

Equation of time-dependent stochastic processes, noted \(X_t\).

They are of the form

\(dx = \underbrace{f(x, t)dt}_{\text{"drift" term}} + \underbrace{g(t) dW_t}_{\text{"diffusion" term}}\),

where \(W_t\) is a “standard Wiener process” or Brownian motion.

They are used in many domains (finance, physics, biology, and even shape analysis)

Differences between SDE and ODE

• Given an initial condition, an SDE has now multiple possible realizations!

• The initial condition is now always \(x_0\), the time only goes Forward

• Solving an SDE means looking for the trajectories density \(p_t(x)\)

Brownian motion

A stochastic process \(W_t\) is a Wiener process, or Brownian motion, if:

• \(W_0 = 0\)
• \(W_t\) is “almost surely” continuous
• \(W_t\) has independent increments
• \(W_t - W_s \sim \mathcal{N}(0, t-s), \text{ for any } 0 \leq s \leq t\)

If we sample 100 trajectories, we obtain: