Emery Pierson, Lei Li, Angela Dai, Maks Ovsjanikov

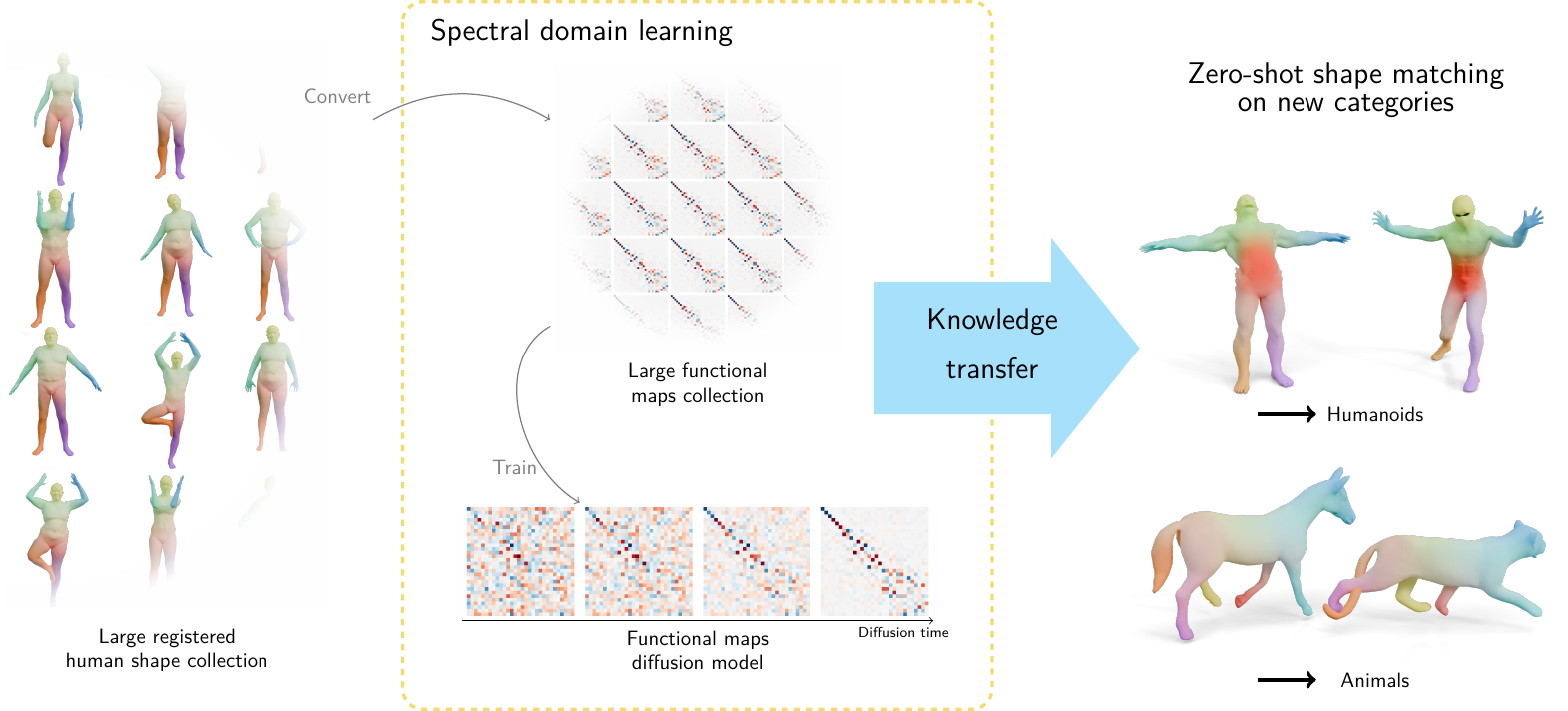
Deep functional maps have recently emerged as a powerful tool for solving non-rigid shape correspondence tasks. Methods that use this approach combine the power and flexibility of the functional map framework, with data-driven learning for improved accuracy and generality. However, most existing methods in this area restrict the learning aspect only to the feature functions and still rely on axiomatic modeling for formulating the training loss or for functional map regularization inside the networks. This limits both the accuracy and the applicability of the resulting approaches only to scenarios where assumptions of the axiomatic models hold. In this work, we show, for the first time, that both in-network regularization and functional map training can be replaced with data-driven methods. For this, we first train a generative model of functional maps in the spectral domain using score-based generative modeling, built from a large collection of high-quality maps. We then exploit the resulting model to promote the structural properties of ground truth functional maps on new shape collections. Remarkably, we demonstrate that the learned models are category-agnostic, and can fully replace commonly used strategies such as enforcing Laplacian commutativity or orthogonality of functional maps. Our key technical contribution is a novel distillation strategy from diffusion models in the spectral domain. Experiments demonstrate that our learned regularization leads to better results than axiomatic approaches for zero-shot non-rigid shape matching.

Approach

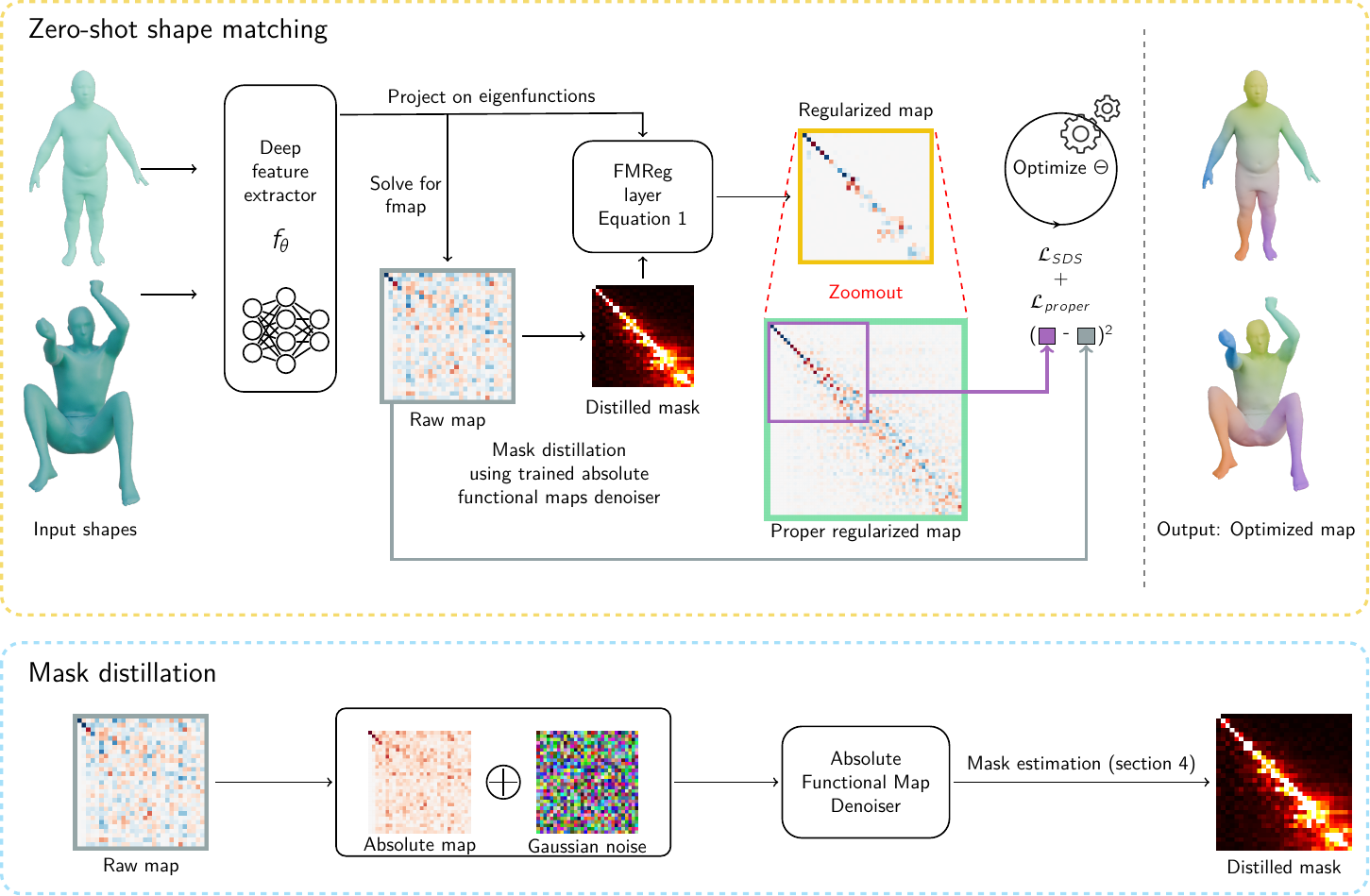
Given a pair of shapes, and a trained spectral functional map model, we train a feature encoder, \(F_i = f_\theta(\mathcal{S}_i)\). We use the features from the encoder in a Siamese way on the two input shapes. Given tentative features we first estimate the functional map \(C\) à la deep functional maps way, with the difference that the regularization mask is distilled from the model. We then evaluate a distillation loss (Eq (13) in the paper) to optimize the parameters of the feature extractor \(f_\theta\) through back-propagation. Once the optimal parameters are computed, we take the associated functional map C and finally convert it to a point to point map through with the standard approach.

Notably, our pipeline differs from previous deep functional maps approaches in that we avoid axiomatic priors, such as Laplacian Commutativity or Orthogonality, both when estimating the mask and applying the training loss. Instead, all of our regularization and objective terms, except for the basic properness term, are derived solely from available training data.

Results

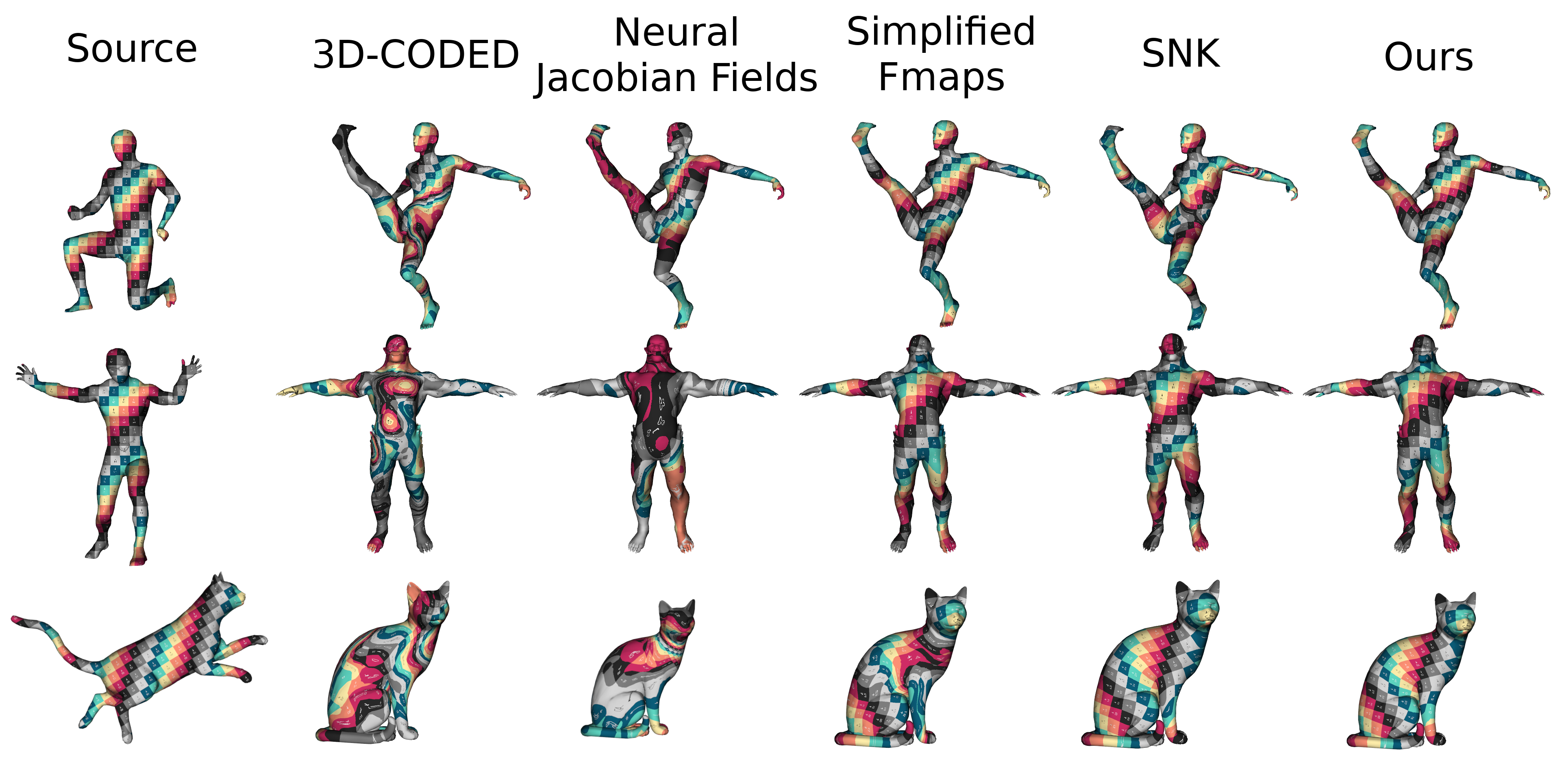
Our method shows the strongest zero-shot capabilities amongs learned methods to new categories, whether they are descriptor or template based.

Acknowledgements

This work was performed using HPC resources from GENCI-IDRIS (Grant 2025-AD010613760R2). Parts of this work were supported by the ERC Consolidator Grant 101087347 (VEGA), as well as gifts from Ansys and Adobe Research, and the ERC Starting Grant SpatialSem (101076253).

Citation

If you consider our work useful, please cite:

**TODO**

This webpage was inspired by Nerfies.