BaRe-ESA: A Riemannian Framework for Unregistered Human Body Shapes

Published in ICCV 2023, Paris, 2023

Emmanuel Hartman, Emery Pierson, Martin Bauer, Nicolas Charon, Mohamed Daoudi

Paper Video Code (experiments coming soon!)


We present Basis Restricted Elastic Shape Analysis (BaRe-ESA), a novel Riemannian framework for human body scan representation, interpolation and extrapolation. BaRe-ESA operates directly on unregistered meshes, i.e., without the need to establish prior point to point correspondences or to assume a consistent mesh structure. Our method relies on a latent space representation, which is equipped with a Riemannian (non-Euclidean) metric associated to an invariant higher-order metric on the space of surfaces. Experimental results on the FAUST and DFAUST datasets show that BaRe-ESA brings significant improvements with respect to previous solutions in terms of shape registration, interpolation and extrapolation. The efficiency and strength of our model is further demonstrated in applications such as motion transfer and random generation of body shape and pose.

Model

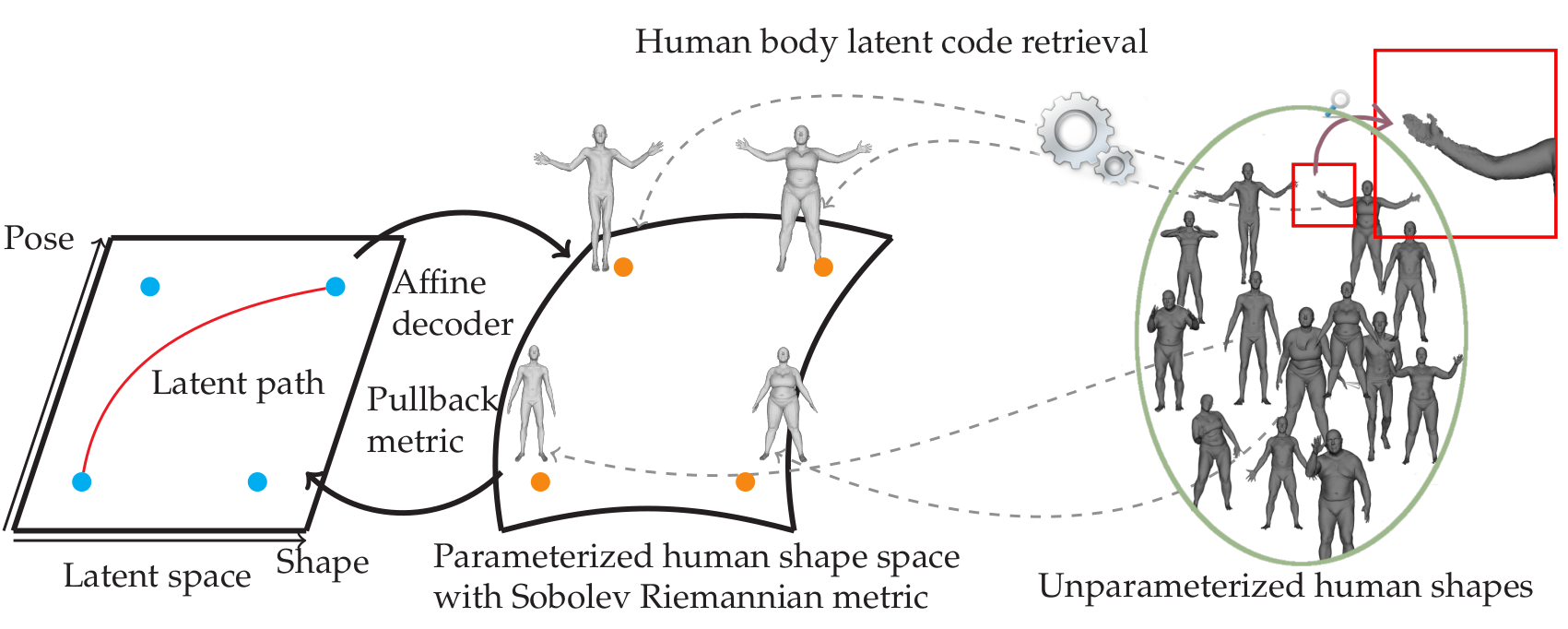
Overwiew of our method. We seek to represent unparameterized human bodies, with different mesh connectivity, and possible noise or topological changes in a disentangled latent space. We define our latent space as the sum of pose and shape spaces. The paths in the latent space are not linear but curved, corresponding to geodesics in the paramaterized human body space. After retrieving the latent codes of the human bodies, we can use the space along with its Riemmanian metric to solve several problems in human body deformation: inter-extrapolation, motion transfer, shape generation.

Our human shape space is defined as :

\[\operatorname{Imm}=\left\{ q\in C^{\infty}(\mathcal{T},\mathbb R^3): Tq \text{ is inj.}\right\}\]

We define a linear Latent space, define as \({\mathcal L}\subset \mathbb R^{n+m}\), with latent vectors \(\alpha\) of human shapes:

\[F(\alpha^j)=\bar q+\sum_{i=1}^m \alpha^j_i h_i+\sum_{i=m+1}^{m+n} \alpha^j_i k_{i-m},\]

where \(\{h_i\}_{i=1}^{m}\) and \(\{k_i\}_{i=1}^n\) are shape and motion basis.

We equipe our latent space with a Riemannian metric:

\[\overline{G}_{\alpha}(\beta,\eta):= G_{F(\alpha)}(F(\beta )-\overline{q},F(\eta )-\overline{q}).,\]

where \(G\) is a weighted Sobolev metric on \(\operatorname{Imm}\) [Hartman et al. 2022].
It has 6 terms, defined as follow:

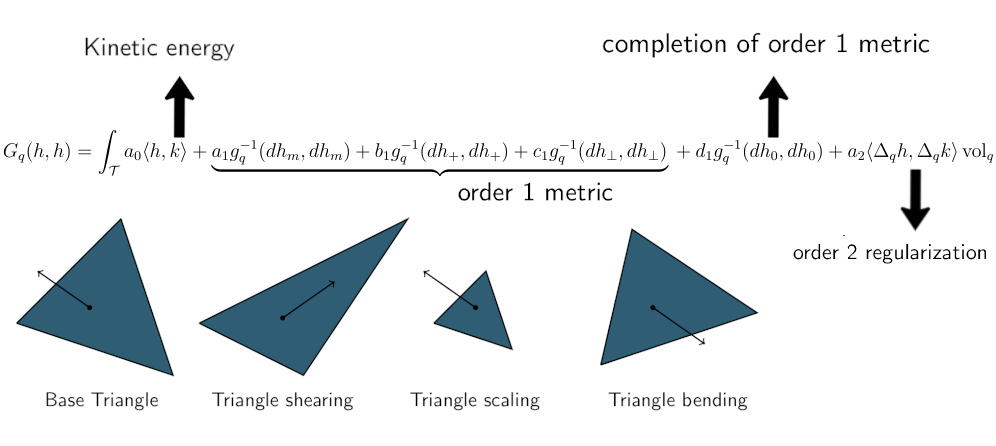
image-center

Where \(a_0, a_1, b_1, c_1, d_1, a_2\) are the metric parameters, set to \(1, 1000, 100, 1, 1, 1\) in this work (penalizing non isometric deformations).

Using this framework, we define interpolation between two shapes \(q_0\) and \(q_1\) as the path \(\alpha(t)\), minimizer of the following energy:

\[\tilde E(\alpha)= \int_0^1 \overline{G}_{\alpha}(\partial_t\alpha,\partial_t\alpha) dt +\lambda \Gamma(F(\alpha)(0),q_0)+\lambda \Gamma(F(\alpha)(1),q_1),\]

where \(\Gamma\) is the varifold [Charon et al. 2013] discrepancy metric, and is equal to 0 when both \(\alpha(i)\) and $q_i$ are reparameterization of each other. This allows to work with unparameterized human shapes.

We can also define extrapolation of the motion of \(q_0\) with inital velocity \(h = q_1 - q_0\) as the solution of the equation:

\[\begin{cases} q(0)&=q_0\\ \partial_t q(0)&=h \end{cases},\]

We solve this equation using a Gauss-Newton scheme (details in the paper).

Video



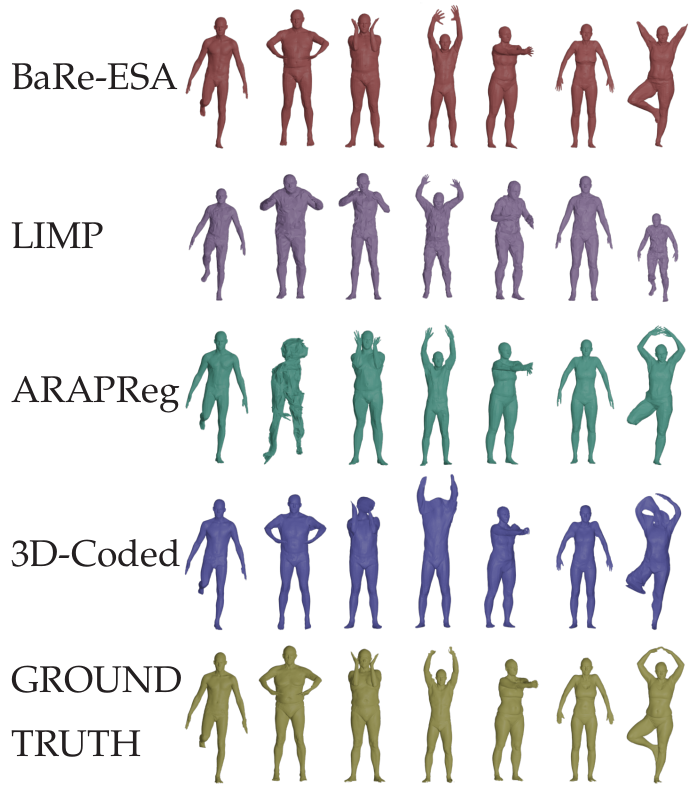
Results (registration)

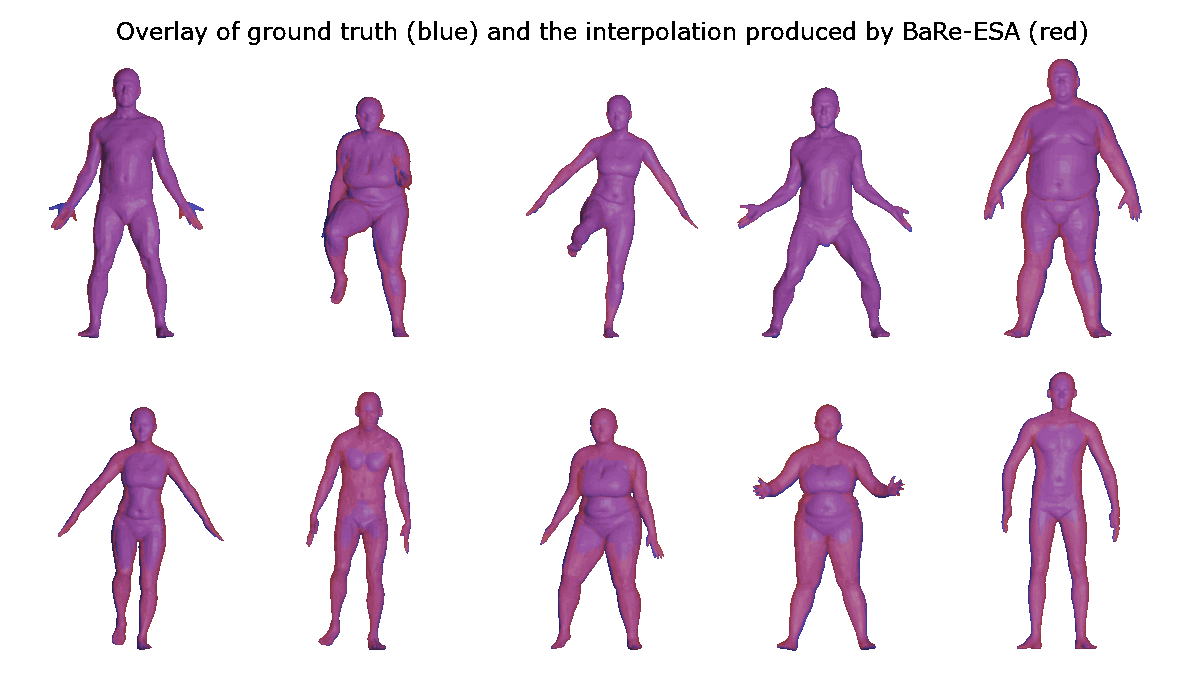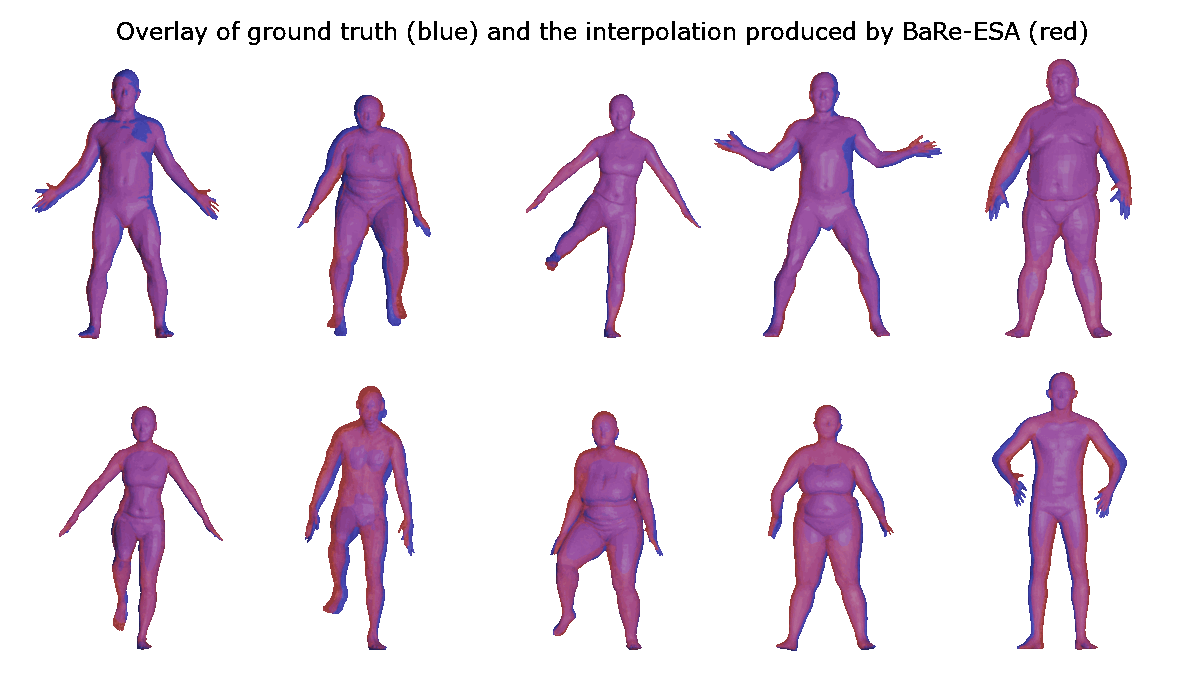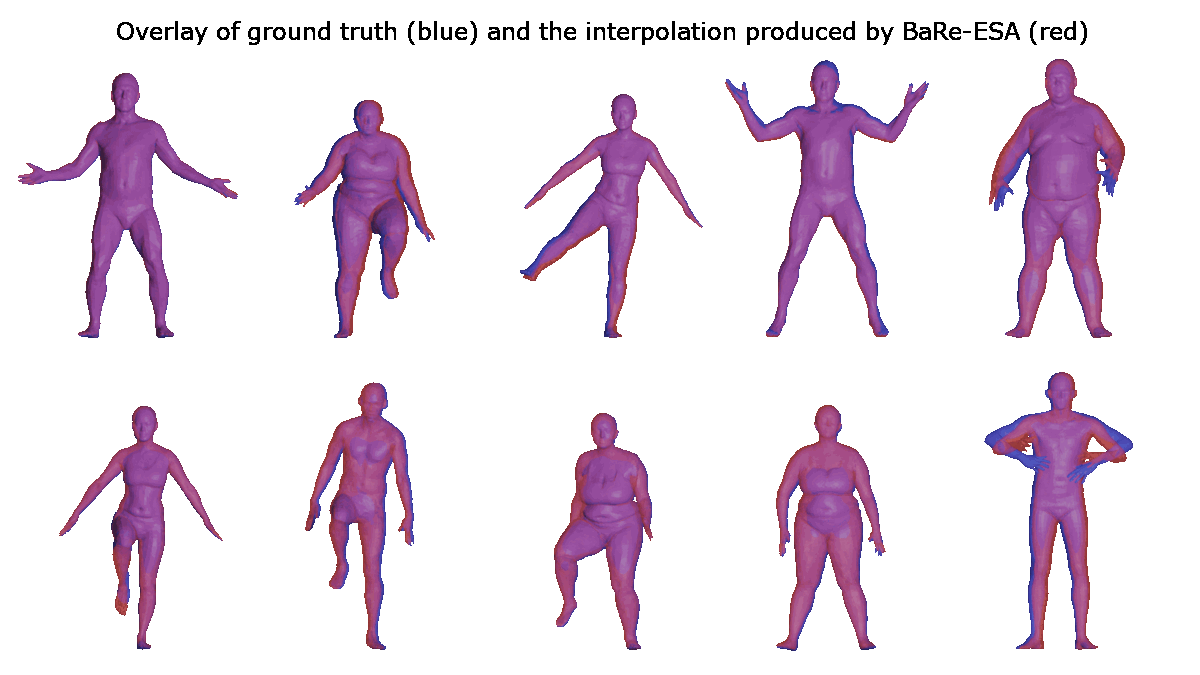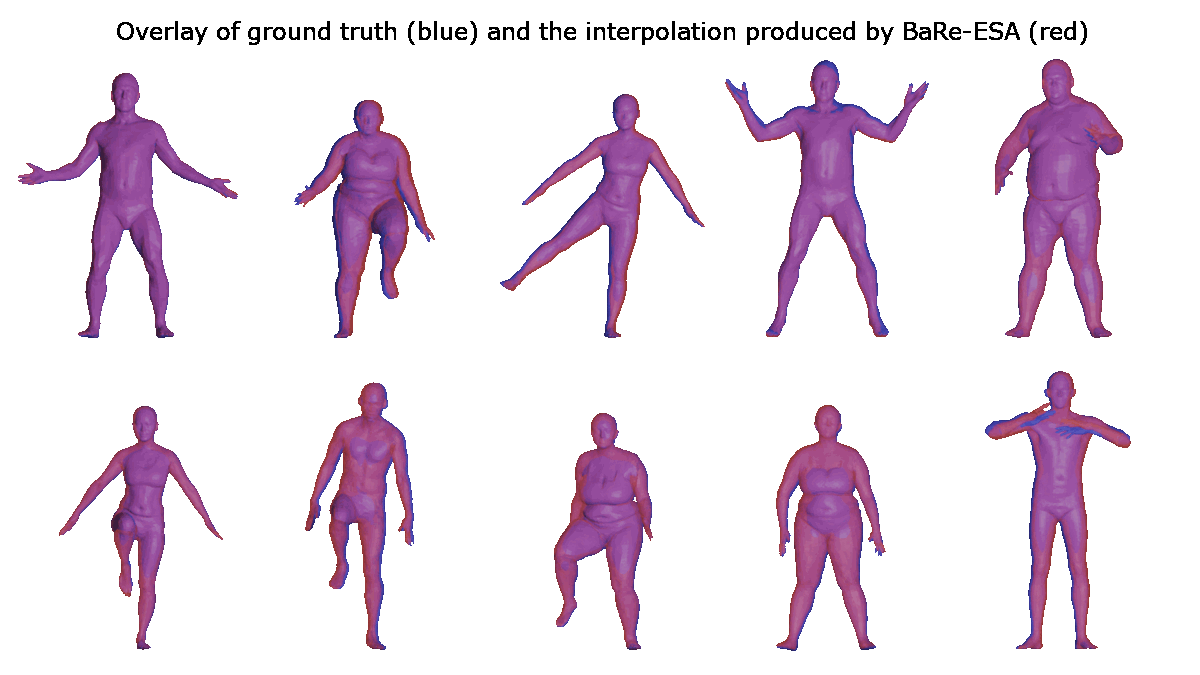
image-center

Results (interpolation)

image-center image-center

Applications

image-center

We can extend our framework to other applications. Motion transfer is done easily via shape code swapping. We can also generate random shapes, by training a generative model on initial velocities from the template shape tangent space (details in the paper).

Acknowledgements

This work was supported by ANR projects 16-IDEX-0004 (ULNE) and by ANR-19-CE23-0020 (Human4D); by NSF grants DMS-1912037, DMS-1953244, DMS-1945224 and DMS-1953267, and by FWF grant FWF-P 35813-N. The training of all methods for the experiments presented in this paper were carried out using the Grid’5000 testbed, supported by a scientific interest group hosted by Inria and including CNRS, RENATER and several Universities as well as other organizations (see https://www.grid5000.fr).

Citation

@article{hartman2022bareesa,
  author    = {Hartman Emmanuel and Pierson Emery and Bauer Martin and Charon Nicolas and Daoudi Mohamed},
  title     = {BaRe-ESA: A Riemannian Framework for Unregistered Human Body Shapes},
  journal   = {ICCV},
  year      = {2023},
}

This webpage was inspired by Nerfies.